Explain Scientific Notation method of measurement.
Text Solution
Chemistry is the study of atoms and molecules which have extremely low masses and are present in extremely large numbers.
A chemist has to deal with numbers as large as 602, 200, 000, 000, 000, 000, 000, 000 for the molecules of 2 g of hydrogen gas or as small as 0.00000000000000000000000166 g mass of a H atom.
Similarly other constants such as Planck.s constant, speed of light, charges on particles etc., involve numbers of the above magnitude.
This problem is solved by using scientific notation for such numbers, i.e., exponential notation in which any number can be represented in the form N×10n where n is an exponent having positive or negative values and N is a number ( called digit term) which varies between 1.000... and 9.999...
e.g. : we can write 232.508 as 2.32508×102 in scientific notation. Similarly, 0.00016 can be written as 1.6×10−4.
Multiplication and Division : These two operation follow the same rules which are there for exponential numbers.
e.g. :1 (5.6×105)×(6.9×108)=(5.6×6.9)(105+8)
=(5.6×6.9)×1013
=38.64×1013
3.864×1014
e.g.: 2 2.7×10−35.5×10−4=(2.7÷5.4)(10−3−4)
=4.909×10−8
Addition and substraction : For these two operations, first the numbers are written in such a way that they have same exponent.
e.g. : Adding 6.65×104 and 8.95×103,6.65×104+0.895×104 exponent is made same for both the number.
Then, these number can be added as follows,
(6.65+0.895)×104=7.545×104
Similarly, the substraction of two numbers can be done as shown below.
2.5×10−2−4.8×10−3=(2.5×10−2)−(0.48×10−2)
=(2.5−0.48)×10−2
=2.02×10−2
|
Topper's Solved these Questions
- SOME BASIC CONCEPTS OF CHEMISTRYBOOK - KUMAR PRAKASHANCHAPTER - SOME BASIC CONCEPTS OF CHEMISTRYEXERCISE - Section - A (Questions) (1.5 Law of Chemical Combinations)
6 Videos
- SOME BASIC CONCEPTS OF CHEMISTRYBOOK - KUMAR PRAKASHANCHAPTER - SOME BASIC CONCEPTS OF CHEMISTRYEXERCISE - Section - A (Questions) (1.6 Dalton.s Atomic Theory)
1 Video
- SOME BASIC CONCEPTS OF CHEMISTRYBOOK - KUMAR PRAKASHANCHAPTER - SOME BASIC CONCEPTS OF CHEMISTRYEXERCISE - Section - A (Questions) (1.3 Properties of Matter and their Measurement)
7 Videos
- SAMPLE QUESTION PAPER FOR FIRST EXAMBOOK - KUMAR PRAKASHANCHAPTER - SAMPLE QUESTION PAPER FOR FIRST EXAMEXERCISE - SECTION -D
2 Videos
- STATES OF MATTER BOOK - KUMAR PRAKASHANCHAPTER - STATES OF MATTER EXERCISE - QUESTION PAPER FROM MODULE (SECTION - A)
4 Videos
Similar Questions
Knowledge Check
Express 0.006006 into scientific notation in three significant digits:
A6.01×10−3B6.006×10−3C6.00×10−3D6.0×10−3
Express 900.00 in scientific notation.
View SolutionWhy is that for both very small as well as very large (in addition to ordinary) quantities, the physical measurements are usually expressed in scientific notation, with powers of ten ?
View SolutionExplain the scientific methods involved in deducing any scientific the theory .
View SolutionExpress the given information in Scientific notation and then arrange them in descending order of their size.
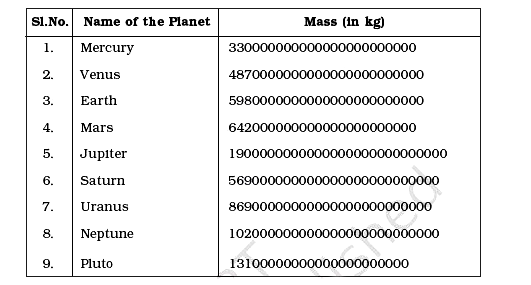
View SolutionThe radius of the sun is 696,0000 m. Express it in scientific notation (in power, of 10).
View SolutionPrecision And Accuracy|Significant Figures|Scientific Notation|Summary
View SolutionExplain measurement of specific heat: Mixing method and calorimeter.
View Solution
