Railway lines are laid with gaps to allow for expansion. If each line is 10 m long at 20∘C, what should be the length of the gap to be kept between two rails to allow for expansion if the maximum temperature that can be reached is 50∘C?
(αsteel=1.2×10−6/∘C)Solution in Marathi
Step by step video & image solution for Railway lines are laid with gaps to allow for expansion. If each line is 10 m long at 20^@C, what should be the length of the gap to be kept between two rails to allow for expansion if the maximum temperature that can be reached is 50^@C? (alpha_(steel)=1.2 xx 10^-6//^@C) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
What is most essential for propagation of mechanical wave?
View SolutionThe dimension for Torque is
View SolutionThe gap between any two rails each of length l laid on a railway trach equals x at 27^@C When the temperature rises to 40^@C the gap closes up. The coefficient of linear expansion of the material of the rail is alpha . The length of a rail at 27^@C will be
View SolutionRailway lines are laid with gaps to allow for expansion. If the gap betweeen steel rails 60 m long be 3.60 cm at 10^(@)C , then at what temperature will the lines just touch? Coefficient of linear expansion of steel =11//10^(-6) .^(@)C^(-1) .
View SolutionA rail track made of steel having length 10 m is clamped on a railway line at its two ends
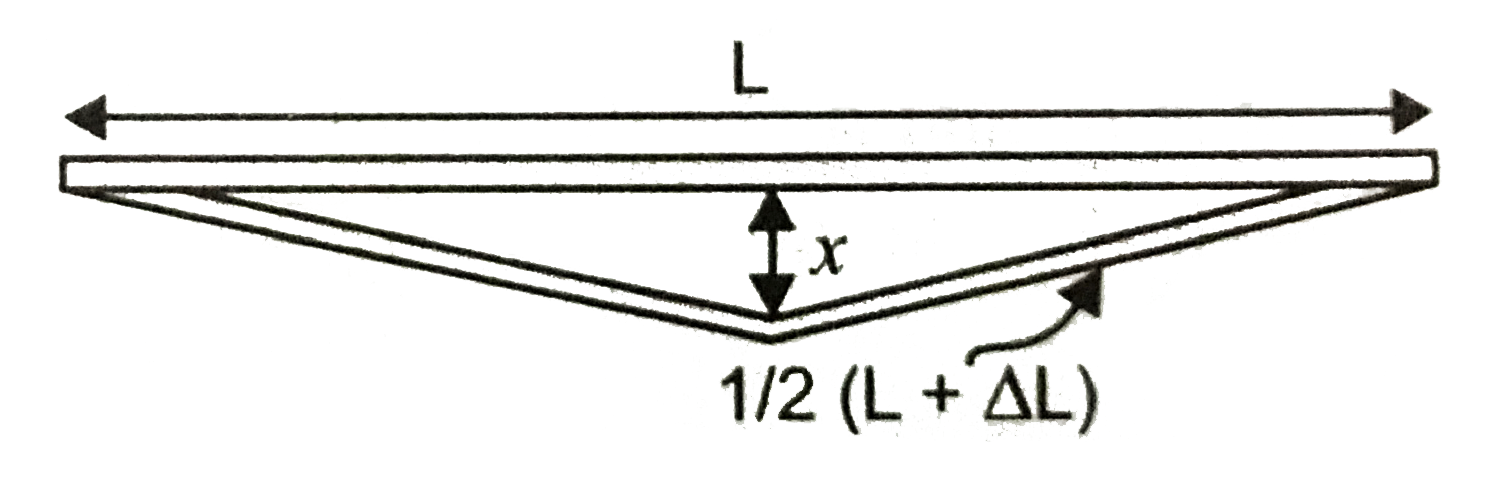
on a summer day due to rise in temperature by 20∘C, it is deformed as shown in fig. Find x (displacement of the centre) if αsteel=1.2×10−5/∘C.
View SolutionThe length of each steel rail is 10m in winter. The coefficient of linear expansion of steel in 0.000012/∘C in summer. The gap to be left between the rails
View SolutionA metre scale made of steel is to be so graduated that at any temperature a reding of 1 mm should be correct up to 0.0005 mm. What can be the maximum allowed change in temperature while marking the millimetre gaps? Coefficient of linear expansion of steel =13.22×10−6∘C−1.
View SolutionThe length of each steel rail of a line at 10^(@)C is 25 m. What gap should be maintained between two successive rails so that up to 50^(@)C they will not be strained? [coefficient of linear expansion of steel =11 times 10^(-6@)C^(-1) ]
View SolutionGaps are left while laying the railway lines in order to allow for expansion. The gap between steel rails of length 65 m is 3.56 cm at 15^@C . Calculate the temperature at which the rails will just touch each other. Take, O_("steel") = 1.1 xx 10^(-5)@C^(-1)
View SolutionA rail track made of steel having length 10 m is clamped on a railway line at its two ends on a summer day due to rise in temperature by 20^@C, it is deformed as shown in fig. Find x (displacement of the centre) if alpha_(steel) = 1.2 xx 10^(-5)//^@C.
View SolutionThe length of each rail is 10m. The linear expansion of steel is 12xx10^(-6)//""^(@)C and range of variation of temperature at the given place is 15^(@)C . The gap to be left between the rails is
View SolutionThe length of each rail is 10m. The linear expansion of steel is 12×10−6/∘C and range of variation of temperature at the given place is 15∘C. The gap to be left between the rails is
View Solution
The gap between any two rails, each of length 'l' laid on a railway track equals x at 27°C. When the temperature rises to 40°C, the gap closes up. The coefficient of linear expansion of material of the rail is 'α'. The length of a rail at 27°C will be
View SolutionRailway lines are laid with gaps to allow for expansion. If the gap between the steel rails 66 m long be 3.63 cm at 10∘C. Then the temperature at which the lines touch (coefficient of linear expansion for steel =11×10−6^(∘)C−1 ) is
View SolutionThe increase in dimensions of a body due to increase in temperature is called thermal expansion.
Railway lines are laid with gaps to allow for expansion.If the gap between steel rails 60m long is 3.63cm at 10°C,then at what temperature will the line just touch?Coefficient of linear expansion for steel is 11×10−6oC
View Solution
