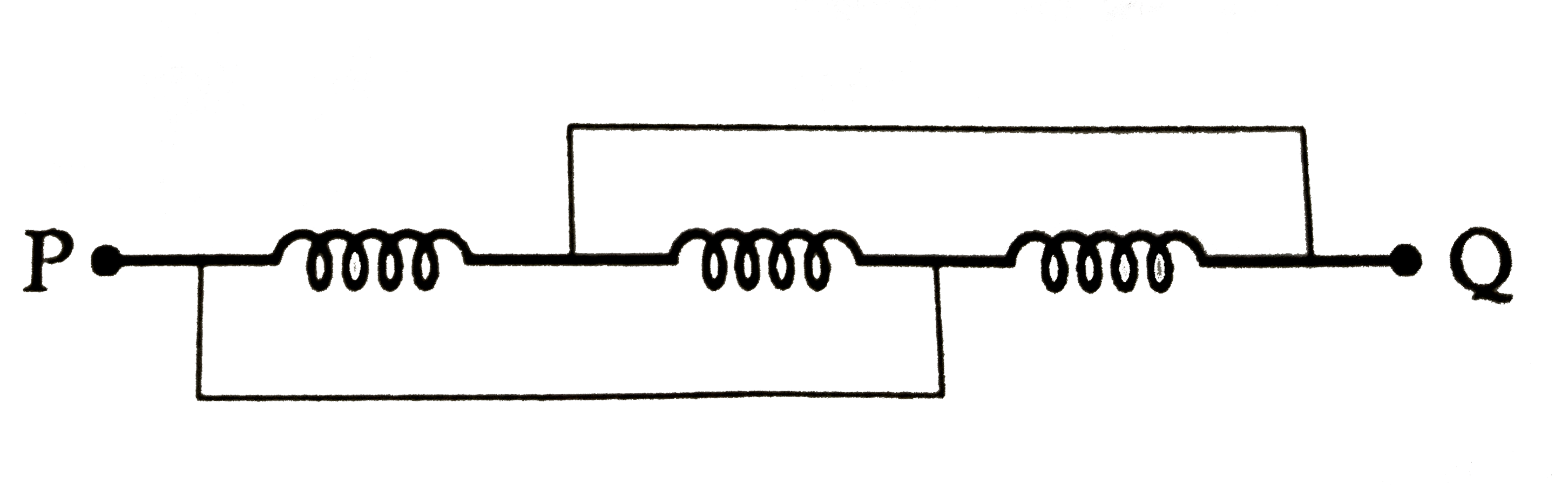
Pure inductances of 3.0 H are connected as shown in figure. The equivalent inductance of the circuit is
A
9H
B
3H
C
1H
D
1/3 H
Text Solution
The correct Answer is:C
The three identical inductances are in parallel.
∴LP=L3=33=1H
|
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT BOOK - MTG-WBJEECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT EXERCISE - WB JEE WORKOUT (Category 2 : Single Option Correct Type)
15 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT BOOK - MTG-WBJEECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT EXERCISE - WB JEE WORKOUT (Category 3: One or More than one Option)
10 Videos
- CURRENT ELECTRICITY BOOK - MTG-WBJEECHAPTER - CURRENT ELECTRICITY EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
21 Videos
- ELECTROMAGNETIC WAVES BOOK - MTG-WBJEECHAPTER - ELECTROMAGNETIC WAVES EXERCISE - WB JEE WORKOUT (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)
10 Videos
Similar Questions
Knowledge Check
Three pure inductors each of 2H are connected as shown in the figure. The equivalent inductance of the circuit is
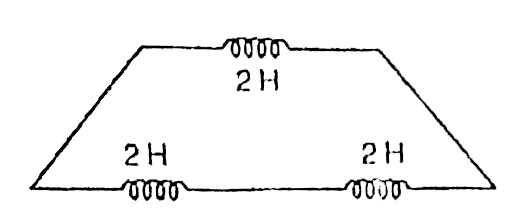 A8H/6B6HC2HDnone of these
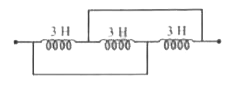
A8H/6B6HC2HDnone of thesePure inductance of 3.0H is connected as shown below. The equivalent inductance of the circuit is
 A1HB2HC3HD9H
A1HB2HC3HD9HTwo inductances connected in parallel are equivalent to a single inductance of 1.5H and when connected in series are equivalent to a single inductance of 0.8 H. The difference in their inductance is
A3 HB7.5 HC2 HD4 H
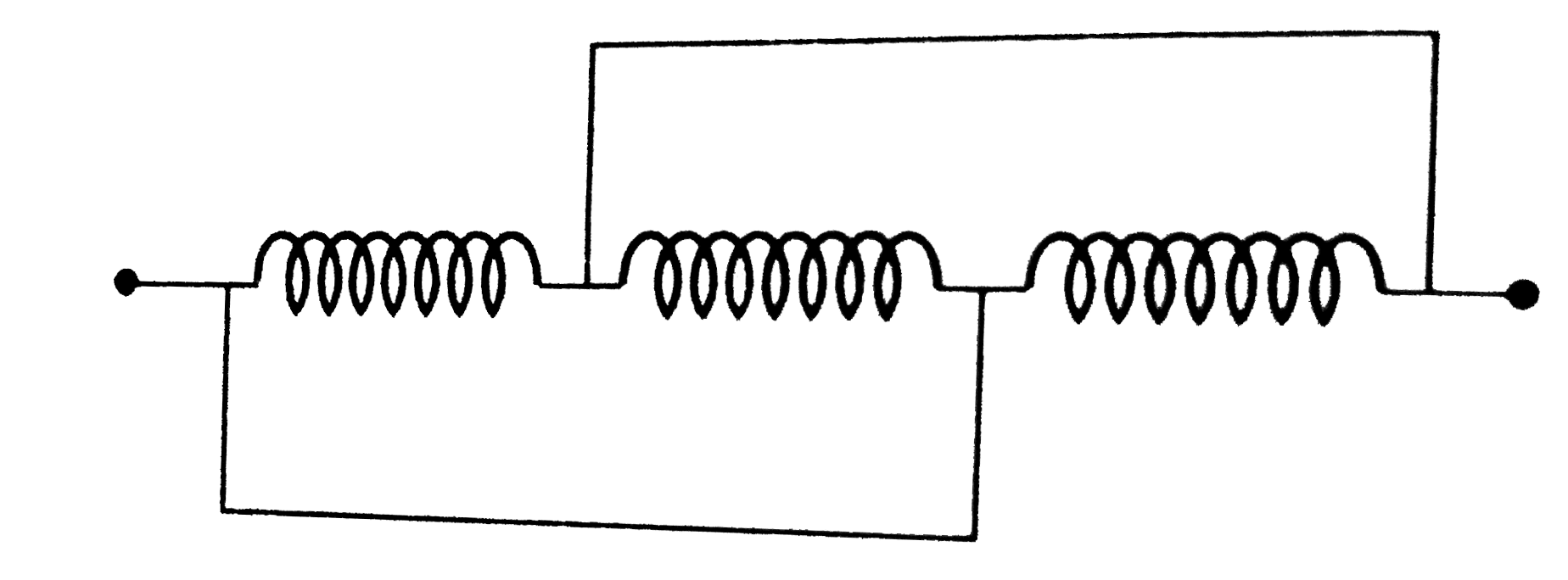
Three pure inductances each of 3H are connected as shown in figure. The equivalent inductance between points A and B is

View SolutionThree inductances are connected as shown in figure. Calculate the resultant inductance.
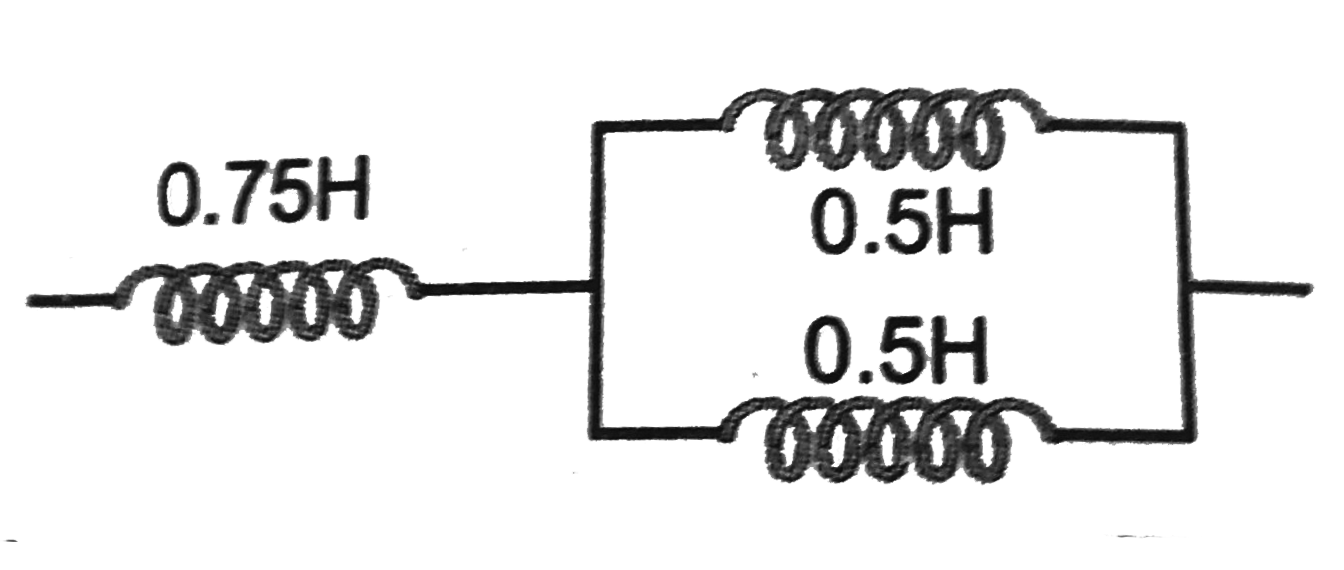
View SolutionTwo inductances connected in parallel are equivalent to a single inductance of 1.5H and when connected in series are equivalent to a single inductance of 8 H. The difference in their inductance is
View SolutionThree inductances are connected as shown below. Assuming no coupling, the resultant inductance will be-

(L1=0.75H,L2=L3=0.5H)
View SolutionMutual inductance in the figure shown is -
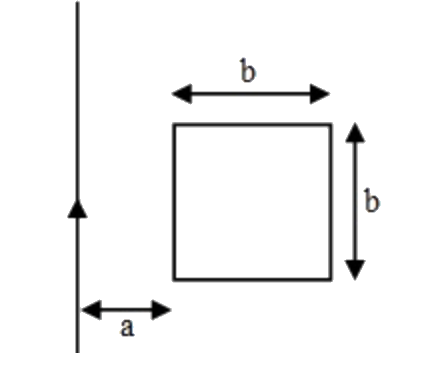
View Solution