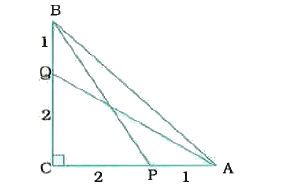
किसी समकोण ΔABC में, ∠C समकोण है , भुजाओं CA तथा CB पर क्रमशः P तथा Q बिंदु हैं , जो की इन भुजाओं 2 : 1 को के अनुपात में विभाजित करते हैं, तो सिद्ध कीजिए कि :
(i) 9AQ2=9AC2+4BC2 (ii ) 9BP2=9BC2+4AC2 (iii) 9(AQ2+BP2)=13AB2
Step by step video & image solution for किसी समकोण Delta ABC में, /_ C समकोण है , भुजाओं CA तथा CB पर क्रमशः P तथा Q बिंदु हैं , जो की इन भुजाओं 2 : 1 को के अनुपात में विभाजित करते हैं, तो सिद्ध कीजिए कि : (i) 9 AQ^(2) = 9AC^(2) + 4BC^(2) (ii ) 9 BP^(2) = 9 BC^(2) + 4AC^(2) (iii) 9 ( AQ^(2) + BP^(2)) = 13 AB^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
माना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solutionइस बिंदु का स्थिति सदिश ज्ञात कीजिए जो कि बिन्दुओ P(3,4,5) तथा Q(6,7,8) को मिलाने रेखा को 2:1 के अनुपात में (i) अंत तथा (ii) बाहा विभाजन करता है।
View SolutionThe right triangle is located at right angle C at ABC. The points P and Q are points on AC and CB respectively and they divide those sides in a 2: 1 ratio. Who 9 (AQ+BP)^(2) = 13AB^(2)
View SolutionIn a right triangle ABC right angled at C, P and Q are points on sides AC and CB respectively which divide these sides in the ratio of 2 : 1.
Prove that (i) 9AQ2=9AC2+4BC2
(ii) 9BP2=9BC2+4AC2
(iii) 9(AQ2+BP2)=13AB2
View SolutionIn a right triangle ABC right angled at C, P and Q are points on sides AC and CB respectively which divide these sides in the ratio of 2 : 1.
Prove that (i) 9AQ2=9AC2+4BC2
(ii) 9BP2=9BC2+4AC2
(iii) 9(AQ2+BP2)=13AB2
View SolutionP and Q are the mid-points of the CA and CD respectively of a triangle ABC, right angled at C. Prove that: 4AQ2=4AC2+ BC2, 4BP2=4BC2+AC2, and 4(AQ2+ BP2)=5AB2.
View SolutionIn a right trianlge ABC right angled at C, P and Q are the points on the sides CA and CB respectively which divide these sides in the ratio 2 : 1. Prove that 9(AQ2+BP2)=13AB2.
View Solution
