A skeleton tube is made of 12 wires each of resistance RΩ is connected to a cell of emf E and of negotiable internal resistance. Use Kirchhoff's laws to find the resistance between:- diagonally opposite corners of the cube.Solution in Marathi
Step by step video & image solution for A skeleton tube is made of 12 wires each of resistance ROmega is connected to a cell of emf E and of negotiable internal resistance. Use Kirchhoff's laws to find the resistance between:- diagonally opposite corners of the cube. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Current ElectricityBook:CHETANA PUBLICATIONChapter:Current ElectricityExercise:Exercise
Explore 92 Videos
- AC CIRCUITSBook:CHETANA PUBLICATIONChapter:AC CIRCUITSExercise:Exercise
Explore 122 Videos
- Dual Nature of Radiation and MatterBook:CHETANA PUBLICATIONChapter:Dual Nature of Radiation and MatterExercise:EXERCISE
Explore 89 Videos
Similar Questions
(1)In the following circuit, calculate the value of the current (I).

View SolutionA LCR series circuit has the impedance of 240 ohm. If R = 120Ω, find the power factor of the circuit.
View SolutionDetermine frequency and wavelength of a photon having energy 1.3eW.
View SolutionA regular hexagon is formed by six wires each of resistance rOmega and the corners are joined to the center by wires of the same resistance. If the current enters at one corner and leaves at the opposite corner, find the equivalent resistance of the conductor.
View SolutionThe terminals of a battery of emf 3 V and internal resistance 2.5Ω are joined to the diagonally opposite corners of a cubical skeleton frame of 12 wires, each of resistance 3Ω. Find the current in the battery.
View SolutionIf n cells each of emf E and internal resistance are connected in parallel, then the total emf and internal resistances will be
View Solution1 ओम प्रतिरोध के बारह तारों को एक घन कंकाल (skeleton cube ) के आकर में जोड़ा गया है । घन विकर्णतः अभिमुख कोनों (diagonally - opposite corners ) के बीच तुल्य - प्रतिरोध की गणना कीजिए । नगण्य आतंरिक प्रतिरोध वाली एक वोल्ट की बैटरी इन कोनों के बीच जोड़ देने से परिपथ में बहने वाली कुल धारा का मान भी ज्ञात कीजिए ।
View SolutionTwelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
View SolutionTwelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
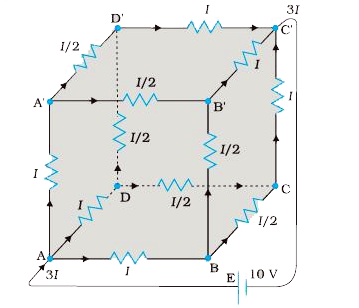
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
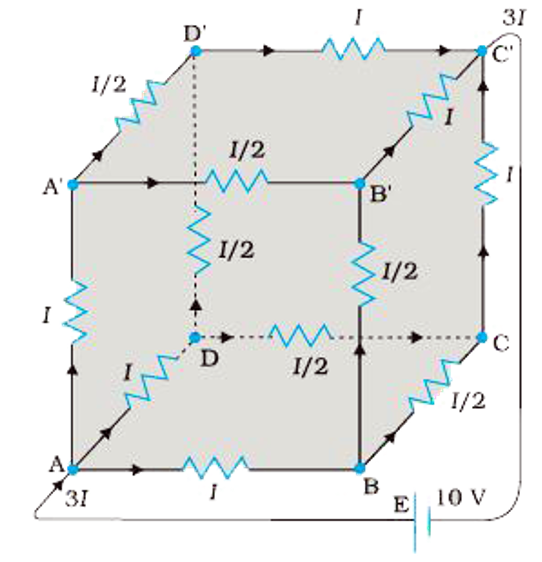
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
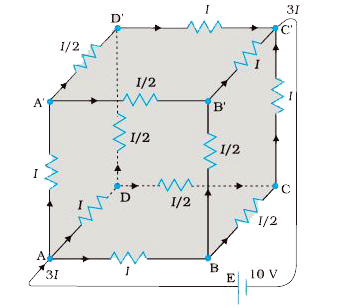
View SolutionIf n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
View SolutionTwelve equal wires each of resistance r are joined to form a skeleton cube. Find the equivalent resistance between two corners on the same edge of the cube.
View SolutionA skeleton tube is made of 12 wires each of resistance RΩ is connected to a cell of emf E and of negotiable internal resistance. Use Kirchhoff's laws to find the resistance between:- diagonally opposite corners of the same face of the cube is across face diagonal.
View Solution