दिखाए गए चित्रानुसार 3K तथा K ऊष्माचालकता गुणांक एवं क्रमश: d तथा 3d मोटाई वाले दो पदार्थों को जोड़कर एक पट्टिका बनायी गयी है। उनके बाहरी सतहों के तापमान क्रमश:θ2 और θ1 हैं (θ2>θ1) अंतरपृष्ठ का तापमान है-
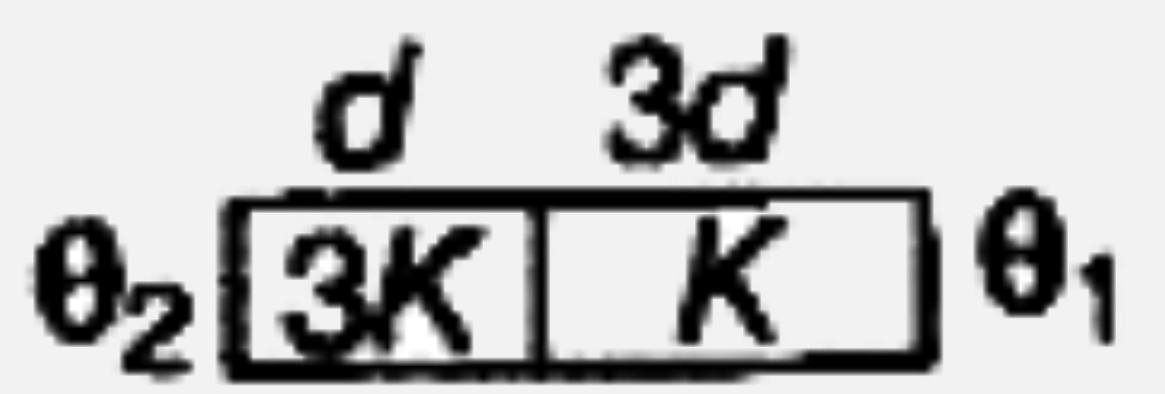
θ16+5θ26
θ13+2θ23
θ2+θ12
θ110+9θ210
The correct Answer is:D
Step by step video & image solution for दिखाए गए चित्रानुसार 3K तथा K ऊष्माचालकता गुणांक एवं क्रमश: d तथा 3d मोटाई वाले दो पदार्थों को जोड़कर एक पट्टिका बनायी गयी है। उनके बाहरी सतहों के तापमान क्रमश:theta_(2) और theta_(1) हैं (theta_(2) gt theta_(1)) अंतरपृष्ठ का तापमान है- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)EXERCISE - APRIL ATTEMPT (10 APRIL, SHIFT-I)
30 Videos
- JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)EXERCISE - APRIL ATTEMPT (10 APRIL, SHIFT-II)
90 Videos
- JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)EXERCISE - APRIL ATTEMPT (9 APRIL, SHIFT-I)
30 Videos
- JEE MAIN 2019BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019EXERCISE - JANUARY ATTEMPT (11 JAN, SHIFT-II )
30 Videos
- JEE MAIN संयुक्त प्रवेश परीक्षा सॉल्वड पेपर 2013 BOOK - ARIHANT HINDICHAPTER - JEE MAIN संयुक्त प्रवेश परीक्षा सॉल्वड पेपर 2013 EXERCISE - MCQ
30 Videos
Similar Questions
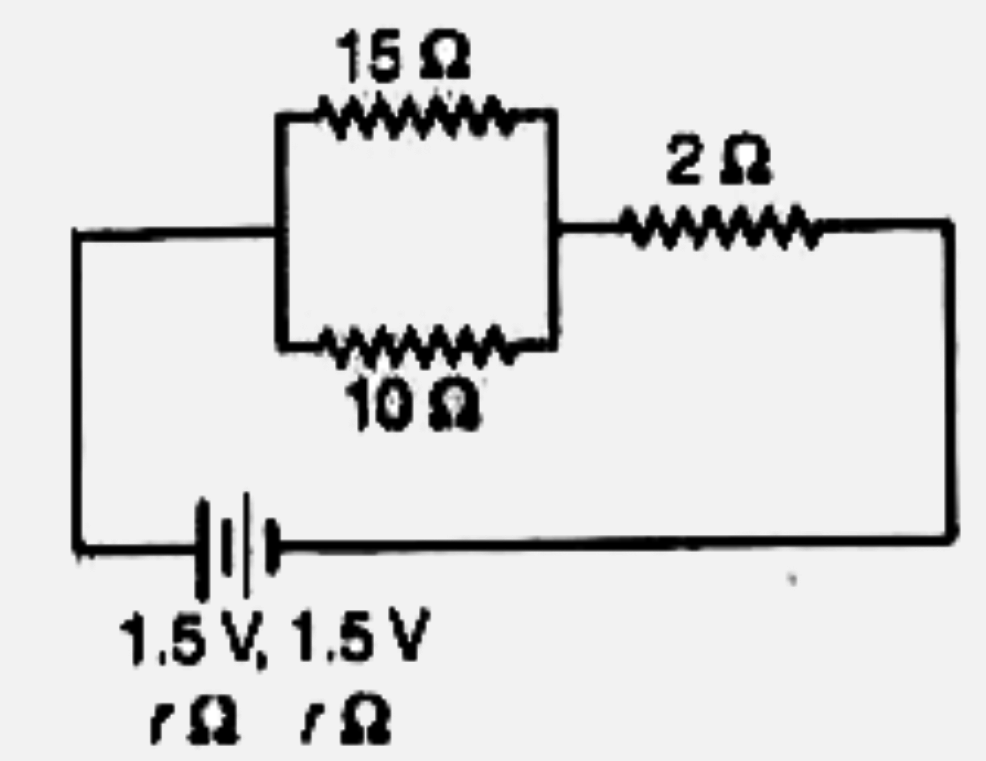
दिए गए परिपथ में एक आदर्श वोल्टमीटर को जब 10Ω प्रतिरोध के सिरों पर लगाते हैं, तो वह 2V मापता है। प्रत्येक सेल का आन्तरिक प्रतिरोध r होगा-
View Solutionएक ग्रह की सतह से 20 किमी ऊँचाई पर एक अन्तरिक्षयान ग्रह के परित: कक्षा में घूम रहा है। यदि यान पर सिर्फ ग्रह का गुरुत्वीय क्षेत्र प्रभावी है, तो यान द्वारा 24 घण्टों में लगाए गए पूरे चक्करों की संख्या का मान होगा (दिया है, ग्रह का द्रव्यमान = 8×1022 किग्रा, ग्रह की त्रिज्या = 2×106 मी, गुरुत्वीय नियतांक, G=6.67×10−11N−m2/kg2)
View Solution5μF धारिता के एक संधारित्र को 5μC तक आवेशित किया जाता है। यदि संधारित्र की प्लेटों को दूर हटाकर उसकी धारिता 2μF कर दी जाए, तो किया गया कार्य होगा |
View Solutionएक m द्रव्यमान का अल्फा कण किसी अज्ञात द्रव्यमान के स्थिर नाभिक से एक-विमीय प्रत्यास्थ संघट्ट करके अपनी प्रारम्भिक गतिज ऊर्जा का 64% भाग क्षय करके ठीक विपरीत दिशा में प्रकीर्णित हो जाता है। नाभिक का द्रव्यमान होगा
View Solutionलम्बाई L, द्रव्यमान M और अनुप्रस्थ परिच्छेद क्षेत्रफल A वाले एकसमान बेलन को इसकी लम्बाई ऊर्ध्वाधर रखते हुए एक द्रव्यमानविहीन कमानी द्वारा एक नियत बिन्दु से इस प्रकार लटकाया गया है कि साम्यावस्था की स्थिति में इसका आधा भाग घनत्व σ के द्रव में डूबा रहे। जब बेलन साम्यावस्था में है, तब कमानी में विस्तार x0 है
View SolutionIf cosθ1=2cosθ2, then tan(θ1−θ22)tan(θ1+θ22) is equal to (a)13 (b) −13 (c)1 (d) −1
View Solutiongiven that tan(theta_(1)+theta_(2))=(tan theta_(1)+tan theta_(2))/(1-tan theta_(1)*tan theta_(2)) find (theta_(1)+theta_(2)) when tan theta_(1)=(1)/(2),tan theta_(2)=(1)/(3)
View Solutionif tan theta_(1)=k cot theta_(2) then find (cos(theta_(1)-theta_(2)))/(cos(theta_(1)+theta_(2)))=
View Solution(cos(theta_(1)-theta_(2)))/(cos(theta_(1)+theta_(2)))+(cos(theta_(3)+theta_(4)))/(cos(theta_(3)-theta_(4)))=0then(tan theta_(1)*tan theta_(2))/(cot theta_(2)*cot theta_(4))
View SolutionIf tanθ1tanθ2=k, then cos(θ1−θ2)cos(θ1+θ2)= 1+k1−k b. 1−k1+k c. k+1k−1 d. k−1k+1
View Solutionf theta_(1),theta_(2),theta_(3),theta_(4),theta_(5)in(0,(pi)/(2)), satisfying tan theta_(1)tan theta_(2)tan theta_(3)tan theta_(4)tan theta_(5)=1 then maximum_(2 value of )theta_(3)tan theta_(4)cos theta_(5) is cos theta_(1)cos theta_(2)cos theta_(3)cos theta_(4)cos theta_(5) is
View SolutionThe angle of a convex pentagon are theta_(1)
View Solutionयदि tan(θ1+θ2)=tanθ1+tanθ21−tanθ1tanθ2,θ1 व θ2 न्यूनकोण है तब θ1+θ2 का मान ज्ञात कीजिए यदि tanθ1=12 व tanθ2=13
View Solutionयदि sinθ1=35,tanθ2=12 तथा π2<θ1<π<θ2, तो सिद्ध कीजिए 8tanθ1−√5secθ2=−72
View SolutionIf cosθ1cosθ2+sinθ1sinθ2=cosθ0cosθ2+sinθ0sinθ2=1, where θ1 and θ0 do not differ by can even multiple of π, prove that
cosθ1⋅cosθ0cos2θ2+sinθ1⋅sinθ0sin2θ2=−1
View SolutionIf tanθ1.tanθ2=k, then: (cos(θ1−θ2)cos(θ1+θ2)=
View Solution
