त्रिज्या R के एक गोले पर आवेश वितरित है, जिसका आयतनिक आवेश घनत्व ρ(R)=Ar2e−2r/a से दिया जाता है, A तथा a नियताक हैं। यदि इस आवेश वितरण का कुल आवेशQ है, तब R त्रिज्या का मान है
alog⎛⎜⎝11−Q2πaA⎞⎟⎠
a2log⎛⎜⎝11−Q2πaA⎞⎟⎠
a2log(1−Q2πaA)
alog(1−Q2πaA)
The correct Answer is:B
Step by step video, text & image solution for त्रिज्या R के एक गोले पर आवेश वितरित है, जिसका आयतनिक आवेश घनत्व rho( R) = A/r^(2)e^(-2r//a) से दिया जाता है, A तथा a नियताक हैं। यदि इस आवेश वितरण का कुल आवेशQ है, तब R त्रिज्या का मान है by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)EXERCISE - JANUARY ATTEMPT (10 JAN, SHIFT -I)
29 Videos
- JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)EXERCISE - JANUARY ATTEMPT (10 JAN, SHIFT -II)
30 Videos
- JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)EXERCISE - JANUARY ATTEMPT (9 JAN, SHIFT -I)
30 Videos
- JEE MAIN 2019BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019EXERCISE - JANUARY ATTEMPT (11 JAN, SHIFT-II )
30 Videos
- JEE MAIN संयुक्त प्रवेश परीक्षा सॉल्वड पेपर 2013 BOOK - ARIHANT HINDICHAPTER - JEE MAIN संयुक्त प्रवेश परीक्षा सॉल्वड पेपर 2013 EXERCISE - MCQ
30 Videos
Similar Questions
2w के एक कार्बन प्रतिरोध को क्रमशः हरे, काले, लाल तथा भूरे रंग में कोड किया गया है। अधिकतम धारा जो इस प्रतिरोध से बह सकती है, होगी |
View Solutionदो बल P तथा Q, जिनके परिमाण क्रमश: 2F तथा 3F हैं, परस्पर θ कोण बनाते हैं। यदि बल Q को दोगुना कर दें, तो इनका परिणामी बल भी दोगुना हो जाता है। तब कोण θ होगा|
View Solutionचिकनी सतह पर रखे m द्रव्यमान के एक गुटके को स्प्रिंग नियतांक की एक कमानी (जिसका द्रव्यमान नगण्य है) से जोड़ा गया है। कमानी का दूसरा सिरा चित्रानुसार अचल है। आरम्भ में गुटका अपनी साम्यावस्था में स्थायी है। यदि गुटके को एक नियत बल F से खींचा जाए, तो गुटके की अधिकतम चाल होगी-
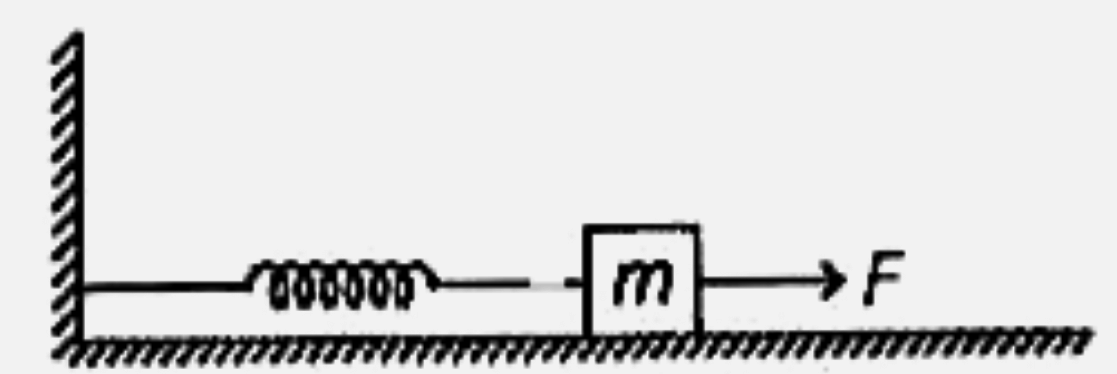
View Solutionएक m द्रव्यमान का अल्फा कण किसी अज्ञात द्रव्यमान के स्थिर नाभिक से एक-विमीय प्रत्यास्थ संघट्ट करके अपनी प्रारम्भिक गतिज ऊर्जा का 64% भाग क्षय करके ठीक विपरीत दिशा में प्रकीर्णित हो जाता है। नाभिक का द्रव्यमान होगा
View Solutionलम्बाई L, द्रव्यमान M और अनुप्रस्थ परिच्छेद क्षेत्रफल A वाले एकसमान बेलन को इसकी लम्बाई ऊर्ध्वाधर रखते हुए एक द्रव्यमानविहीन कमानी द्वारा एक नियत बिन्दु से इस प्रकार लटकाया गया है कि साम्यावस्था की स्थिति में इसका आधा भाग घनत्व σ के द्रव में डूबा रहे। जब बेलन साम्यावस्था में है, तब कमानी में विस्तार x0 है
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionदो विधुतरूधर ताँबे के समरूप आवेशित गोलों A और B में क्रमश: qA और qB आवेश है। उसी साइज का तीसरा अनावेशित गोला C पहले गोले A के संपर्क में रखा जाता है। तथा उसके बाद गोले B के संपर्क में रखा जाता है। अंत में दोनों से दूर कर दिया जाता है। A और B में नए आवेश क्या होंगे ?
View Solutionयदि z−αz+α(α∈R) एक शुद्ध रूप से काल्पनिक संख्या है तथा |z|=2 है तो α का एक मान है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionयदि .8Cr−.7C3=.7C2, तब r का मान है
View Solutionउस गोले का सदिश समीकरण ज्ञात कीजिए जिसका केन्द्र (2,-3,4) तथा त्रिज्या 5 है।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जिसका केंद्र (3,2,1) तथा त्रिज्या 5 है।
View Solutionयदि गोले का संदिश समीकरण r^(2) - vec( r ) . ( 8vec( i ) - 6 vec( j ) + 10 vec( k )) - 50 = 0 है तो गोले का केंद्र और त्रिज्या ज्ञात कीजिए।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जिसका केन्द्र (2, 2, 1 ) तथा त्रिज्या 4 है।
View Solutionयदि गोले का व्यास 14 से. मी. है, तो उसकी त्रिज्या होगी-
View Solutionआवेश के विशिष्ट गुण|आवेश एक अदिश राशि है|आवेश सदैव द्रव्यमान के साथ सम्बन्ध होता है|महतवपूर्ण बिंदु|आवेश का स्थानांतरण|आवेश का क्वांटिकरण|आवेश संरक्षित है|OMR|Summary
View Solution
