The equation for displacement of S.H.M. is given by Y=AX_____Solution in Odia
Step by step video & image solution for The equation for displacement of S.H.M. is given by Y=AX_____ by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If the tube length of astronomical telescope is 1.5 cm and magnifying power is 20 for normal setting, calculate the focal length of the objective.
View SolutionUsing dimensional method, show that 1N=105 dynes.
View SolutionPart of a simple harmonic motion is graphed in the figure, where y is the displacement from the mean position. The correct equation describing this S.H.M is-
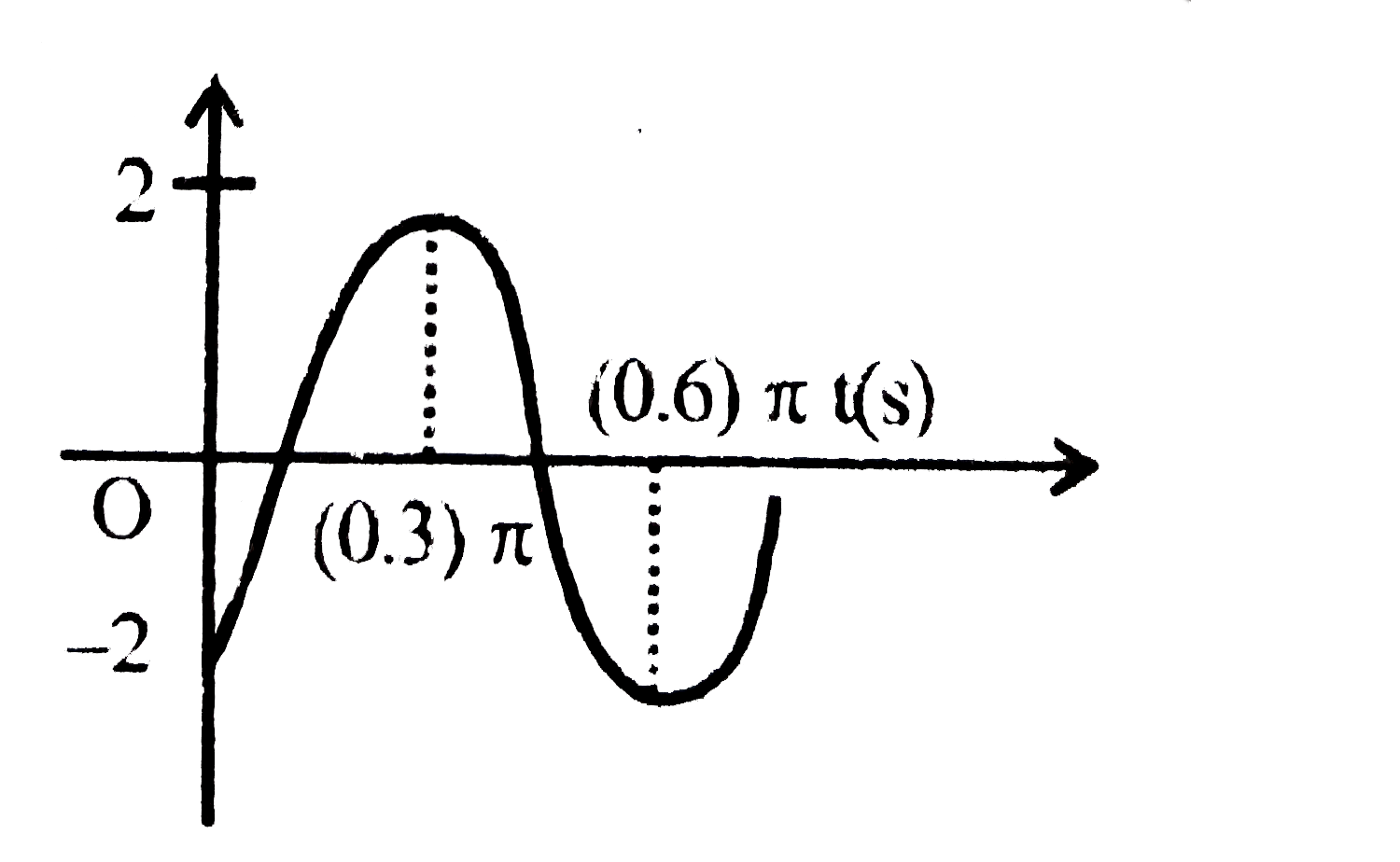
View SolutionThe average displacement over a period of S.H.M. is (A = amplitude of S.H.M)
View SolutionThe displacement of a particle executing S.H.M. is given by y=10sin[6t+π3] where y is in metres and t is in seconds. Then the initial displacement and velocity of the particle is
View SolutionThe displacement of a particle performing a S.H.M is given by x=0.25 "cos"[8πt+π3]. The frequency of S.H.M. is
View SolutionThe displacement of a particle performing S.H.M. is given by x=10 "sin"(omega t+ alpha) metre. If the displacement of the particle is 5m, then the phase of S.H.M. is
View SolutionThe displacement of a particle executing S.H.M. is given by, y = 0.20 sin (100 t) cm. The maximum speed of the particle is
View SolutionGiven equation of S.H.M. is y = 10 sin(20t+0.5). The initial phase is
View SolutionThe displacement in S.H.M. is given by y=asin(20t+4). What is the displacement it is increased by 2π/ω?
View SolutionThe displacement of a particle executing S.H.M. is given by y = 0.25 sin 200t cm. The maximum speed of the particle is
View SolutionThe displacement equation of a particle executing S.H.M is given by y=0.01sinπ(t+0.005)m. Calculate the maximum velocity and displacement at the time of start of the motion.
View SolutionThe displacement of a particle executing S.H.M. is given by, y = 0.20 sin (100 t) cm. The maximum speed of the particle is
View SolutionGiven equation of S.H.M. is y = 10 sin(20t+0.5). The initial phase is
View SolutionFrom the differential equation of linear S.H.M. obtain expressions for acceleration, velocity and displacement of particle performing S.H.M.
View Solution
