Take a square ABCD of side l and BD is diagnol. Find MOI along a line passing through corner parallel to BD
3ml2
2ml2
ml2
4ml2
To find the moment of inertia (MOI) of a square ABCD of side length l about a line passing through one corner (let's say corner A) and parallel to the diagonal BD, we can follow these steps:
Step 1: Understand the Configuration
We have a square ABCD with vertices A, B, C, and D. The diagonal BD divides the square into two equal triangles. We need to find the moment of inertia about a line through point A parallel to BD.
Step 2: Identify the Mass Distribution
Assume each corner of the square has a mass m. The coordinates of the corners can be defined as:
- A(0, 0)
- B(l, 0)
- C(l, l)
- D(0, l)
Step 3: Determine the Distances
Since the line of inertia passes through point A and is parallel to diagonal BD, we need to calculate the perpendicular distances from the other points (B, C, and D) to this line.
- The distance from point A to the line is 0 (since the line passes through A).
- The distance from point B to the line (parallel to BD) is l√2.
- The distance from point C to the line is l√2.
- The distance from point D to the line is l.
Step 4: Calculate the Moment of Inertia for Each Mass
Using the formula for moment of inertia I=∑mir2i, where ri is the distance from the axis of rotation to the mass mi:
1. For mass at point A:
IA=m⋅02=0
2. For mass at point B:
IB=m⋅(l√2)2=m⋅l22
3. For mass at point C:
IC=m⋅(l√2)2=m⋅l22
4. For mass at point D:
ID=m⋅l2
Step 5: Sum the Moments of Inertia
Now, we sum all the contributions to the moment of inertia:
I=IA+IB+IC+ID
I=0+m⋅l22+m⋅l22+m⋅l2
I=m⋅l22+m⋅l22+m⋅l2=m⋅(l22+l22+l2)
I=m⋅(2⋅l22+l2)=m⋅(l2+l2)=3ml2
Final Result
Thus, the moment of inertia of the square about the line passing through corner A and parallel to diagonal BD is:
I=3ml2
We have a square ABCD with vertices A, B, C, and D. The diagonal BD divides the square into two equal triangles. We need to find the moment of inertia about a line through point A parallel to BD.
Assume each corner of the square has a mass m. The coordinates of the corners can be defined as:
- A(0, 0)
- B(l, 0)
- C(l, l)
- D(0, l)
Since the line of inertia passes through point A and is parallel to diagonal BD, we need to calculate the perpendicular distances from the other points (B, C, and D) to this line.
- The distance from point B to the line (parallel to BD) is l√2.
- The distance from point C to the line is l√2.
- The distance from point D to the line is l.
Using the formula for moment of inertia I=∑mir2i, where ri is the distance from the axis of rotation to the mass mi:
IA=m⋅02=0
IB=m⋅(l√2)2=m⋅l22
IC=m⋅(l√2)2=m⋅l22
ID=m⋅l2
Now, we sum all the contributions to the moment of inertia:
I=IA+IB+IC+ID
I=0+m⋅l22+m⋅l22+m⋅l2
I=m⋅l22+m⋅l22+m⋅l2=m⋅(l22+l22+l2)
I=m⋅(2⋅l22+l2)=m⋅(l2+l2)=3ml2
Thus, the moment of inertia of the square about the line passing through corner A and parallel to diagonal BD is:
I=3ml2
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Moment of inertia of a square plate of side l about the axis passing through one of the corner and perpendicular to the plane of square plate is given by :
View SolutionABCD is a square of side length 2 units. C1 is the circle touching all the sides of the square ABCD and C2 is the circumcircle of square ABCD. L is a fixed line in the same plane and R is fixed point.
A line L' through a is drawn parallel to BD. Point S moves scuh that its distances from the line BD and the vertex A are equal. If loucs S cuts L' at T2andT3 and AC at T1, then area of ΔT1T2T3 is
View Solution
Knowledge Check
Four point masses, each of value m, are placed at the corners of a square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is
A3ml2Bml2C2ml2D√3ml2Four point masses, each of value m, are placed at the corners of a square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is
A√3ml2B3ml2Cml2D2ml2Four point masses, each of value m, are placed at the corners of square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is -
A2ml2B√3ml2C3ml2Dml2
Let ABCD be a square of side length 2 units. C2 is the circle through vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A
A line M through A is drawn parallel to BD. Point S moves such that its distances from the line BD and the vertex A are equal. If locus of S cuts. M at T2 and T3 and AC at T1, then area of ΔT1T2T3 is
View SolutionLet ABCD be a square of side length 2 units. C2 is the circle through vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A
A line M through A is drawn parallel to BD. Point S moves such that its distances from the line BD and the vertex A are equal. If locus of S cuts. M at T2 and T3 and AC at T1, then area of ΔT1T2T3 is
View SolutionFour point masses, each of value m, are placed at the corners of a square ABCD of side 1. The moment of inertia of this system about an axis through A and parallel to BD is
View SolutionFour point masses each of value m, are placed at the corners of a square ABCD of side l, The moment of inertia of the system about an axis passing throught A and parallel to BD is
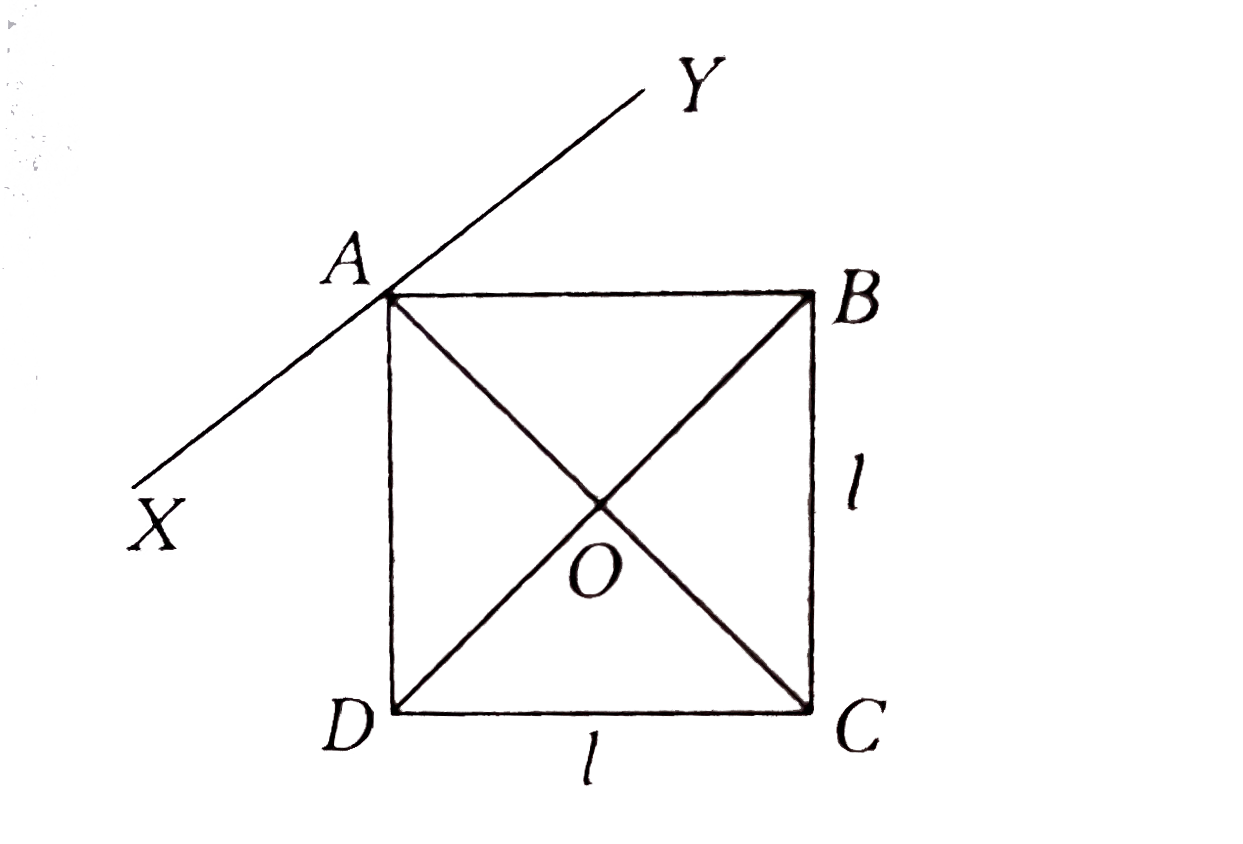
View SolutionFour point masses, each of value m, are placed at the corners of a squre ABCD of side l. The moment of inertia of the is system about an axis passing through A and parallel to BD is
View Solution
