Four vector and are lying in the same plane. The vectors and are equal in magnitude and inclined to each other at an angle of . is the resultant of and . Further . If the angle between and is and the angle between and is , find the correct relation between and
The correct Answer is:
Topper's Solved these Questions
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - Numerical Exercise( Level 2)
21 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Questions for Descriptive Answers
10 Videos
- EXPANSION OF GASESBOOK - AAKASH SERIESCHAPTER - EXPANSION OF GASESEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
Similar Questions
Four vectors ¯a,¯b,¯c,and¯d are lying in the same plane. The vectors ¯a and ¯b are equal in magnitude and inclined to each other at an angle of 120∘.¯¯¯C is the resultant of ¯aand¯b. Further ¯a+¯b+¯d=0. If the angle between ¯aand¯dis β and the angle between ¯aand¯cis a, find the correct relation between α and β
View SolutionIf ¯a,¯b,¯c are unit vectors such that ¯a.¯b=0,¯a.¯c and the angle between ¯band¯c is π3 then the value of ∣∣¯aׯb−¯aׯc∣∣ is _______
View Solution
Knowledge Check
Non-zero vectors ¯a,¯b and ¯c are related by ¯a=8¯b and ¯c=−7¯b.
Then the angle between ¯a and ¯c isAπ4Bπ2CπD0The non-zero vectors ¯a,¯b and ¯c are related by ¯a=8¯b and ¯c=−7¯b. Then, the angle between ¯a and ¯c is of measures
A0Bπ4Cπ2DπIF ¯a,¯b,¯cand¯d are any four vectors then (¯aׯb)×(¯cׯd) is a vector
Aperpendicular to ¯a,¯b,¯cand¯dBalong the line of intersection of two planes, one containing ¯a,¯b other containing ¯c,¯dCequally inclined to both ¯aׯband¯cׯdDNone of these
Let ¯a,¯b,¯c are the three vectors such that ∣∣¯a}=∣∣¯b∣∣=|¯c|=2 and angle between ¯aand¯bisπ/3,¯band¯cisπ/3 and ¯aand¯cπ/3.
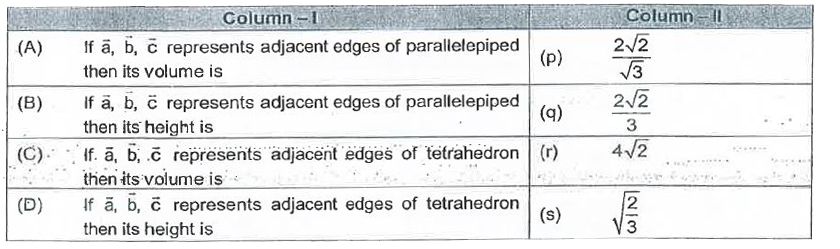
View SolutionIf A(¯a),B(¯b),C(¯c) and D(¯d) are the four points such that 3¯a+8¯b=6¯c+5¯d, then the lines AB and CD are
View SolutionIf ¯a,¯b,¯care three coplanar vectors, then [¯a+¯b ¯b+¯c ¯c+¯a]=
View SolutionIf ¯a,¯b,¯c be any three non-coplanar vectors, then [¯a+¯b ¯b+¯c ¯c+¯a]=
View SolutionIf ¯aand¯b be parrallel vectors, then [¯a ¯c ¯b]=
View Solution
