Two particles each of mass .m. move in a circle of radius the action of their mutual gravitational attraction of each particle is
√Gmr
√Gm4r
√Gm2r
√2Gmr
The correct Answer is:B
Topper's Solved these Questions
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - PRACTICE SHEET (EXERCISE-I) Kepler.s laws and Newton law of gravitation (LEVEL-II) Straight Objective Type Questions
6 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - PRACTICE SHEET (EXERCISE-I) Kepler.s laws and Newton law of gravitation (LEVEL-II) More than One correct answer Type Questions
1 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - LECTURE SHEET (EXERCISE=-IV) Gravitational Field, potential & satellite energy (Integer Type Questions )
4 Videos
- GAUSS.S LAW BOOK - AAKASH SERIESCHAPTER - GAUSS.S LAW EXERCISE - PROBLEMS (LEVEL - II)
12 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
Similar Questions
Four particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
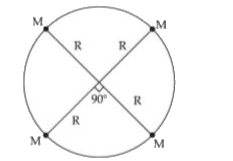
View SolutionTwo particles of equal mass (m) move in a circle of radius (r ) under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution
Knowledge Check
Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A√GMRB√2√2GMRC√GMR(1+2√2)D12√GMR(1+2√2)Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
AGmRB√2√2GMRC√GMR(2√2+1)D√GMR2√2+14Two particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
AV=12R√1GmBV=√GM2RCV=12√GmRDV=√4GmR
_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.
View Solution_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.
View SolutionTwo particles of equal masses m go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is v=√GmnR. Find the value of n.
View SolutionTwo particles of equal masses m go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is v=√GmnR. Find the value of n.
View SolutionTwo particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
View Solution
