यदि tanθ=pq तो दिखाइए कि psinθ−qcosθpsinθ+qcosθ=p2−q2p2+q2
Step by step video & image solution for यदि tantheta=(p)/(q) तो दिखाइए कि (p sintheta-qcostheta)/(p sintheta+qcostheta)=(p^(2)-q^(2))/(p^(2)+q^(2)) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमितीय BOOK - S CHANDCHAPTER - त्रिकोणमितीय EXERCISE - प्रश्नावली 27.2
31 Videos
- त्रिकोणमितीय BOOK - S CHANDCHAPTER - त्रिकोणमितीय EXERCISE - प्रश्नावली 27.3
11 Videos
- त्रिकोणमितीय BOOK - S CHANDCHAPTER - त्रिकोणमितीय EXERCISE - साधित उदाहरण
43 Videos
- ज्यामितीय रचनाएँBOOK - S CHANDCHAPTER - ज्यामितीय रचनाएँEXERCISE - प्रश्नावली 26.2
14 Videos
- त्रिभुज BOOK - S CHANDCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 18.2 रिक्त स्थानों को भरे :
5 Videos
Similar Questions
निम्नलिखित में से प्रत्येक के मान ज्ञात कीजिए :
sin60∘cos30∘+cos60∘sin30∘
View Solutionत्रिभुज ABC में कोण B समकोण है। त्रिभुज के शेष अवयव ज्ञात कीजिए यदि :
∠C=45∘,AB=5 सेमी
View Solutionमान ज्ञात कीजिए
sin60∘cos30∘−cos60∘sin30∘
View Solutionएक त्रिभुज के आधार की लंबाई 5cm दो शेष भुजाओं की लंबाई का योग 7.8cm है तथा इसका आधार कोण 60∘ है, तो परिमाप होगा।
View Solutionयदि ∠ACD=124∘,∠ABC=36∘, तो ∠BAC=………….
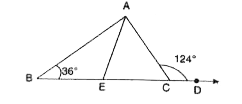
View SolutionIf psinθ+qcosθ=aandpcosθ−qsinθ=b, show that : p+aq+b+q−bp−a=0.
View SolutionIf tanθ=pq, then the value of psinθ−qcosθpsinθ+qcosθ is
View SolutionIf sinθ+cosθ=pandsecθ+cosθ=q, then prove that q(p2−1)=2p
View Solutionनिम्नलिखित को सर्वसमिकाओ की सहायता से सिद्ध कीजिए।
Q.यदि secθ+tanθ=p हो तो सिद्ध करो की P2−1P2+1=sinθ
View SolutionIf tanθ=pq then find the value of psinθ−qcosθpsinθ+qcosθ
View SolutionIf sinθ+cosθ=pandtanθ+cotθ=q,thenq(p2−1) is equal to
View SolutionLet P and Q be 3×3 matrices with P≠Q . If P3=Q3andP2Q=P2Q=Q2P, then determinant of (P2+Q2) is equal to :
View SolutionP∗q=p2−q2
p$q=p2−q2
p$q=p2+q2
p∘q=pq+p+q
pΔq = Remainder of pq
p©q = greatest integer less than or equal to pq.
If p=8andq=10 , then the value of [(p$q)Δ(p∘q)]∗[(q∗p)∘(q©p)] is :
View SolutionP∗q=p2−q2
p$q=p2+q2
p∘q=pq+p+q
pΔq = Remainder of pq
p©q = greatest integer less than or equal to pq.
If p=15andq=25, then the value of the expression [(q∗p)∘(p$q)] is:
View SolutionIf secA=x+14xprove that:
secA+tanA=2xor12x
(b) If tanθ=pq,show that :
psinθ−qcosθpsinθ+qcosθ=p2−q2p2+q2
View SolutionIf sintheta +costheta =p And sectheta +"cosec" theta= q Then prove that p^2 -1 = (2p)/q
View Solution
