ধরা যাক, f(x)=ax(a>0) অপেক্ষকটিকে f(x) = g(x)+h(x) রূপে লেখা হল যেখানে g(x) একটি যুগ্ম অপেক্ষক এবং h(x) একটি অযুগ্ম অপেক্ষক| তাহলে g(x+y)+g(x-y) এর মান
2g(x)g(y)
এনসিওমারের জোড়
2g(x)
g(x)h(X)
Step by step video & image solution for ধরা যাক, f(x)=a^x(agt0) অপেক্ষকটিকে f(x) = g(x)+h(x) রূপে লেখা হল যেখানে g(x) একটি যুগ্ম অপেক্ষক এবং h(x) একটি অযুগ্ম অপেক্ষক| তাহলে g(x+y)+g(x-y) এর মান by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
একটি গোল টেবিলের সঙ্গে চারটি বিভিন্ন রং-এর চেয়ার আছে | চারটি ছেলেকে ওই টেবিল ঘিরে কত ভাবে বসানো যায়?
View SolutionIf f(x-y)=f(x).g(y)-f(y).g(x) and g(x-y)=g(x).g(y)+f(x).f(y) for all x in R. If right handed derivative at x=0 exists for f(x) find the derivative of g(x) at x=0
View SolutionIf y=∣∣ ∣ ∣∣f(x)g(x)h(x)lmnabc∣∣ ∣ ∣∣ , prove that dydx=∣∣f′(x)g′(x)h′(x)lmnabc∣∣ .
View SolutionIf f(x), g(x), h(x) are polynomials of three degree, then phi(x)=|(f'(x),g'(x),h'(x)), (f''(x),g''(x),h''(x)), (f'''(x),g'''(x),h'''(x))| is a polynomial of degree (where f^n (x) represents nth derivative of f(x))
View SolutionLet f,g,h be differentiable functions of x. if Δ=∣∣ ∣ ∣∣fgh(xf)'(xg)'(xh)'(x2f)''(x2g)''(x2h)''∣∣ ∣ ∣∣and,Δ'=∣∣ ∣ ∣∣fghf'g'h'(xnf'')'(xng'')'(xnh'')'∣∣ ∣ ∣∣, then n =
View SolutionIf f(x) be a function such that f(−x)=−f(x),g(x) be a function such that g(−x)=−g(x) and h(x) be a function such that h(−x)=h(x), then choose the correct statement:
I. h(f(g(−x)))=−h(f(g(x)))
II. f(g(h(−x)))=f(g(h(x)))
III. g(f(−x))=g(f(x))
View SolutionIf f(x)=sinx,g(x)=x2andh(x)=logx, find h[g{f(x)}].
View SolutionIf f(x)=4x−5,g(x)=x2andh(x)=1x, then f(g(h(x))) is :
View SolutionIf the three functions f(x),g(x) and h(x) are such that h(x)=f(x).g(x) and f'(x).g'(x)=c, where c is a constant then f''(x)f(x)+g''(x)g(x)+2cf(x)⋅g(x) is equal to
View SolutionIf f(x−y)=f(x).g(y)−f(y).g(x) and g(x−y)=g(x).g(y)+f(x).f(y) for all x∈R . If right handed derivative at x=0 exists for f(x) find the derivative of g(x) at x =0
View SolutionGraph of y=f(x)andy=g(x) is given in the following figure. If h(x)=f(g(x)), then find the value of h'(2).
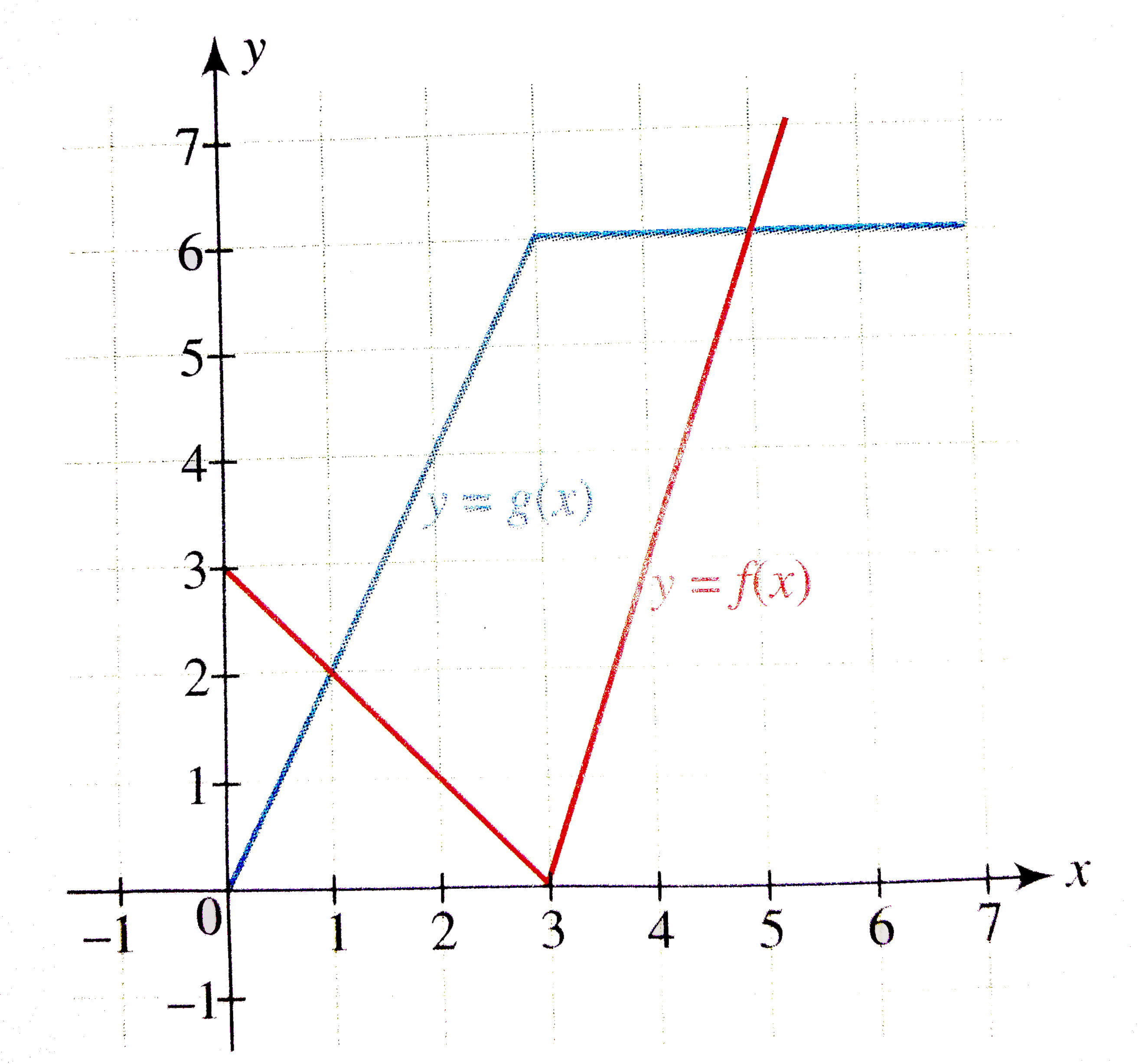
View SolutionIf f(x−y)=f(x).g(y)−f(y).g(x) and g(x−y)=g(x).g(y)+f(x).f(y) for all x∈R . If right handed derivative at x=0 exists for f(x) find the derivative of g(x) at x =0
View SolutionIf f(x),g(x)sin^(-1)x And h(x)=f(g(x)) , Then h'(x)//h(x)=
View Solutionयदि f(x)=ex,g(x)=sin−1x और h(x)=f(g(x)), तब h'(x)/h(x)=
View Solutionf(x)=x,g(x)=1x and h(x)= f(x) g(x). If h(x) = 1 then…….
View SolutionIf f(x),g(x),h(x) are polynomials in x of degree 2 If F(x)=∣∣ ∣ ∣∣fghf'g'h'f''g''h''∣∣ ∣ ∣∣
then F'(x) is
View Solution
