f:[−2,2]→R একটি সন্তত অপেক্ষক এবং f(x) সর্বদাই অমূলদ | যদি f(√2)=√2 হয় তবে
2
f(√2−1)=√2−1
f(√2−1)=√2+1
f(√2−1)=√2
Step by step video & image solution for f:[-2,2]rightarrowR একটি সন্তত অপেক্ষক এবং f(x) সর্বদাই অমূলদ | যদি f(sqrt2)=sqrt2 হয় তবে by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
√x+1−√x−1=√4x−1 সমীকরণটির সমাধানের সংখ্যা হল
View Solutionযদি y2−4y=4x−4a এর শীর্ষবিন্দু সব সময় x+y=3 এবং 2x+2y−1=0 সরল রেখা দুটির মধ্যবর্তী অঞ্চলে অবস্থান করে তবে
View SolutionNumber of point where function f(x) defined as f:[0,2π]→R,f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩3−∣∣∣cosx−1√2∣∣∣,|sinx|<1√22+∣∣∣cosx+1√2∣∣∣,|sinx|≥1√2 is non differentiable is
View SolutionIf f(x) = x√x , then f(√2)=
View SolutionIf f(x) = 0 when x is an integer.
= 2 when x is not an integer,
then find - (a) f(0), (b) f(√2).
View SolutionThe constant c of Rolle's theorem for the function f(x)=2x3+x2−4x−2 in [−√2,√2] is
View Solutionf:Nto[-sqrt2,sqrt2]:f(x)=sinx+cosx , then f(x) is
View Solutionমনে করো, A একটি 2×2ক্রমেরম্যাট্রিক্স,এবংA^2=0 (যেখানে0একটিশূন্যম্যাট্রিক্স,)I 2times2ক্রমেরএককম্যাট্রিক্সতবে−যদিA!=০এবংA= [[a,b],[c,d]] , ad-bc=0এবংA^2-(a+d)A+(ad-bc)I =0হয়,তবেa+d এর মান হবে-
View Solutionf(x)=x2−1x−1অপেক্ষকেরলেখচিত্রঅঙ্কনকরােএবংx = 1ওx= 2 বিন্দুতে অপেক্ষক সন্তত কি না তা লেখচিত্র থেকে বলাে।
View SolutionLet f:[−2,2]→R be a continuous function such that f(x) assumes only irrationlal values. If f(√2)=√2. Then
View SolutionLet f(x)=√2−(cosx+sinx)1−sin2x,x≠π/4. The value f(π/4) so that f is continuous is (√2=1.41)
View SolutionNumber of point where function f(x) defined as f:[0,2π]→R,f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩3−∣∣∣cosx−1√2∣∣∣,|sinx|<1√22+∣∣∣cosx+1√2∣∣∣,|sinx|≥1√2 is non differentiable is
View SolutionLet f:R→R be such that f(x)=2x . Determine: Range of f (ii) {x:f(x)=1} (iii) Whether f(x+y)=f(x)f(y) holds.
View SolutionFind f(√2) and f(−√3) for the function
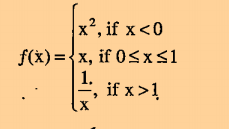
View SolutionLet f[−2,2]→R be a continuous function such that f(x)assumes only irrational values. If f(√2)=√2,
View SolutionIf f (x) =αxx+1 , x ≠−1 , for what value of αis f[f(x)] = x?
a)√2 b)−√2 c)1 d)-1
View Solution
