माना बिन्दुओ A, B, C के निर्देशांक (acosθ1,asinθi)i=1,2,3द्वारा निरूपित किये जाते है तथा cs(θ1−θ2)+cos(θ2−θ3)+cos(θ3−θ1)=−32 है
1 : ΔABC का लम्बकेन्द्र (0, 0) है।
2 : ΔABC एक समबाहु त्रिभुज है।
कथन- 1 सत्य है , कथन - 2 सत्य यही, कथन-2 कथन-1 का सही स्प्ष्टीकरण है।
कथन- 1 सत्य है, कथन-2 सत्य है, कथन-2 कथन-1 का सही स्पष्टीकरण ugh है।
कथन-1 सत्य है, कथन-2 असत्य है।
कथन-1 असत्य है, कथन-2 सत्य है।
The correct Answer is:A
Step by step video, text & image solution for माना बिन्दुओ A, B, C के निर्देशांक (a cos theta_(1), a sin theta _(i)) i = 1, 2, 3 द्वारा निरूपित किये जाते है तथा cs (theta_(1) - theta_(2)) + cos (theta_(2) - theta_(3)) + cos (theta_(3) - theta_(1)) = - (3)/(2) है 1 : Delta ABC का लम्बकेन्द्र (0, 0) है। 2 : Delta ABC एक समबाहु त्रिभुज है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - BANSAL HINDICHAPTER - सरल रेखा EXERCISE - Exercise - (Special Dpp - 7 ) Paragraph2videos
सरल रेखा
- BOOK - BANSAL HINDICHAPTER - सरल रेखा EXERCISE - Exercise - (Special Dpp - 8 )11videos
सरल रेखा
- BOOK - BANSAL HINDICHAPTER - सरल रेखा EXERCISE - Exercise - (Special Dpp - 6 ) Paragraph11videos
सरल रेखा
- BOOK - BANSAL HINDICHAPTER - सदिश एवं त्रिविम निर्देशांक ज्यामितीय (VECTOR & 3-D)EXERCISE - EXERCISE-5 (RANK BOOSTER)13videos
सदिश एवं त्रिविम निर्देशांक ज्यामितीय (VECTOR & 3-D)
Similar Questions
एक समबाहु त्रिभुज ABC का केन्द्रक मूल बिन्दु (0,0) पर है तथा इसका आधार BC रेखा x + y = 1 के अनुदिश है, तो
समबाहु ΔABC का क्षेत्रफल है01:37View Solutionरेखाओ |x| + |y| = 2 द्वारा निर्मित चतर्भुज का क्षेत्रफल है
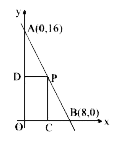
02:10View Solutionचित्र में दिखाये अनुसार, बिन्दुओ A(0, 16) तथा B(8,0) से गुजरने वाली एक रेखा खींची जाती है। A एवं B से गुजरने वाली रेखा पर प्रथम चतुर्थांश में एक बिन्दु P लिया जाता है। x एवं y-अक्ष पर क्रमशः बिन्दु c एवं D इस प्रकार लिये जाते है कि PDOC एक आयत है।
रेखा AB की बिन्दु (2, 2) से लम्बवत् दुरी है
 01:35View Solution
01:35View Solutionकिसी चतुष्फलक के शीर्ष A,B,C की स्थिति सदिश क्रमशः (1,1,1),(1,0,0) तथा (3,0,0) है। यदि शीर्ष D से विपरीत तल ABC पर लंब डाला जाता है तथा यह त्रिभुज ABC के शीर्ष A से जाने वाली माध्यिका पर बिंदु E पर मिलता है। यदि AD की लम्बाई 4 तथा चतुष्फलक का आयतन 2√23 है। तो E की स्थिति ज्ञात कीजिए।
06:17View SolutionIf sinθ1+sinθ2+sinθ3=3, then cosθ1+cosθ2+cosθ3 is equal to
(a) 3
(b) 2
(c) 1
(d) 001:48View SolutionIf ABC having vertices A(acosθ1,asinθ1),B(acosθ2asinθ2),andC(acosθ3,asinθ3) is equilateral, then prove that cosθ1+cosθ2+cosθ3=sinθ1+sinθ2+sinθ3=0.
02:48View SolutionIf (acosθ1,asinθ1),(acosθ2,asinθ2) and (acosθ3,asinθ3) represent the vertices of an equilateral triangle inscribed in a circle, then (a) cosθ1+cosθ2+cosθ3=0 (b) sinθ1+sinθ2+sinθ3=0 (c) tanθ1+tanθ2+tanθ3=0 (d) cotθ1+cotθ2+cotθ3=0
02:08View SolutionIF A(cosθ1,sinθ1),B(cosθ2,sinθ2)&C(cosθ3,sinθ3), then Orthocenter of ΔABC is
05:18View SolutionIf sinθ1+sinθ2+sinθ3, then find the value of cosθ1+cosθ2+cosθ3.
02:48View SolutionIf (cos theta_(1),sin theta_(1)),B(cos theta_(2),sin theta_(2)) and C(cos theta_(3),sin theta_(3)) then orthocenter of Delta ABC is
06:34View SolutionIf (acosθ1,asinθ1),(acosθ2,asinθ2),(acosθ3,asinθ3) represents the vertices of an equilateral triangle inscribed in x2+y2=a2, then
05:41View SolutionIf cosθ1cosθ2+sinθ1sinθ2=cosθ0cosθ2+sinθ0sinθ2=1, where θ1 and θ0 do not differ by can even multiple of π, prove that
cosθ1⋅cosθ0cos2θ2+sinθ1⋅sinθ0sin2θ2=−102:02View Solutionयदि sinθ1+sinθ2+sinθ3+sinθ4=4, है cosθ1+cosθ2+cosθ3+cosθ4 का मान है
02:43View SolutionIf θ1,θ2,θ3....,θn are in A.P. then sinθ1+sinθ2+...+sinθncosθ1+cosθ2+...+cosθn=
03:11View SolutionIf cos(θ1−θ2)cos(θ1+θ2)+cos(θ3+θ4)cos(θ3−θ4)=0 then
tanθ1.tanθ2.tanθ3.tanθ4=07:33View Solution

