Question

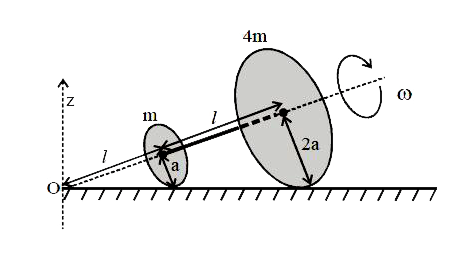
m तथा 4m द्रव्यमान वाली दो पतली वृत्ताकार चत्रिकाएँ (discs), जिनकी त्रिज्याऐं क्रमशः a तथा 2a हैं, के केन्द्रों को $l=\sqrt{24}a$  लम्बाई की द्रव्यमान-रहित द्रढ़ (rigid) डंडी से जोड़ा गया है। इस समूह को एक मजबूत समतल सतह पर लिटाया गया है और फिसलाये बिना इस तरह से घुमाया गया है कि इसकी कोणीय गति डंडी के अक्ष के गिर्द $\omega$ है । पूरे समूह का बिन्दु $\text{'}\omega \text{'}$ के गिर्द कोणीय संवेग $\overrightarrow{L}$ है (चित्र देखिये) । निम्नलिखित में से कौनसा/कौनसे कथन सत्य है /हैं ?
 

Options

A. पूरे समूह के संहति केंद्र का बिन्दु O के गिर्द कोणीय संवेग का परिमाण `81 ma^2 omega`
B. पूरे समूह का उसके संहति केंद्र के गिर्द कोणीय संवेग का परिमाण `17ma^2 omega//2`
C. पूरे समूह का संहति केन्द्र z-अक्ष के गिर्द कोणीय वेग `omega//5`से घूम रहा है
D. `vecL` के z-घटक का परिमाण `55ma^2 omega` है

Answer

B::C