ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਰੇਖੀ ਸਮੀਕਰਨਾਂ ਨੂੰ ਹੱਲ ਕਰੋ 3t−24−2t+33=23−t
Step by step video & image solution for ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਰੇਖੀ ਸਮੀਕਰਨਾਂ ਨੂੰ ਹੱਲ ਕਰੋ (3t-2)/4-(2t+3)/3=2/3-t by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ਇੱਕ ਚਲ ਵਾਲੇ ਰੇਖੀ ਸਮੀਕਰਨ Book:PSEB (PUNJABI MEDIUM)Chapter:ਇੱਕ ਚਲ ਵਾਲੇ ਰੇਖੀ ਸਮੀਕਰਨ Exercise:EXERCISE
Explore 65 Videos
- ਅੰਕੜਿਆਂ ਦਾ ਪ੍ਰਬੰਧਨBook:PSEB (PUNJABI MEDIUM)Chapter:ਅੰਕੜਿਆਂ ਦਾ ਪ੍ਰਬੰਧਨExercise:EXAMPLE
Explore 2 Videos
- ਖੇਤਰਮਿਤੀ Book:PSEB (PUNJABI MEDIUM)Chapter:ਖੇਤਰਮਿਤੀ Exercise:EXAMPLE
Explore 10 Videos
Similar Questions
x-2=7
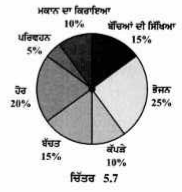
View Solutionਨਾਲ ਦਿੱਤਾ ਪਾਈ ਚਾਰਟ (ਚਿੱਤਰ 5.7) ਇੱਕ ਮਹੀਨੇ ਵਿੱਚ ਇੱਕ ਪਰਿਵਾਰ ਦੇ ਵੱਖ-ਵੱਖ ਮੱਦਾਂ ਵਿੱਚ ਖਰਚੇ ਅਤੇ ਉਸਦੀ ਬੱਚਤ (ਪ੍ਰਤੀਸ਼ਤਾਂ ਵਿੱਚ) ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ। ਕਿਸ ਮੱਦ ਵਿੱਚ ਖਰਚ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਸੀ ?
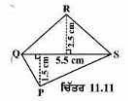
View Solutionਚਿੱਤਰ 11.11 ਵਿੱਚ ਦਰਸਾਏ ਗਏ ਚਤੁਰਭੁਜ PQRS ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ।
View Solutionsolve the equation . 3t−24−2t+33=23−t
View Solution(3t-2) / (4) - (2t + 3) / (3) = (2) / (3) -t
View SolutionThe parametric equations of the curve are x=2t(t^(2)+3)-3t^(2),y=2t(t^(2)+3)+3t^(2) Find the maximum slope of the curve and the corresponding point on it.
View SolutionSolve : 3t−24−2t+33=23−t
View Solution3t−24−2t+33=23−t
View SolutionIf x=2t+3t2,y=t2+2t3, then: (y1)2+2(y1)3=
View SolutionIf S=(t^(3))/(3)-2t^(2)+3t+4 , then
View SolutionCheck whether the first polynomial is a factor of the second polynomial by dividing :
t2−3,2t4+3t3−2t2−9t−12
View SolutionIF x=t2+2t,y=t3−3t, where t is a parameter then show that, d2ydx2=34(t+1).
View Solution3t−24−2t+33=23−t
View SolutionCheck whether the first polynomial is a factor of the second polynomial by dividing :
t2−3,2t4+3t3−2t2−9t−12
View SolutionSolve : 3t−24−2t+33=23−t
View SolutionSolve the following linear equations.
3t−24−2t+33=23−t
View Solution
