Angular velocity of a ring is ω. If we put two masses each of mass m at the diametrically opposite points then the resultant angular velocity (m=mass of ring)
The correct Answer is:ω'=ω3
To solve the problem of finding the resultant angular velocity of a ring with two masses added at diametrically opposite points, we can follow these steps:
1. Understand the System:
We have a ring with an initial angular velocity ω and a mass m. Two additional masses, each of mass m, are placed at diametrically opposite points on the ring.
2. Identify the Moment of Inertia:
The moment of inertia I of a ring about its center is given by:
Iring=mR2
where R is the radius of the ring.
3. Calculate the Moment of Inertia of the Added Masses:
Each mass m is located at a distance R from the center of the ring. Since there are two masses, the total moment of inertia contributed by the two masses is:
Imasses=2⋅mR2=2mR2
4. Total Moment of Inertia:
The total moment of inertia Itotal of the system (ring + two masses) is:
Itotal=Iring+Imasses=mR2+2mR2=3mR2
5. Apply Conservation of Angular Momentum:
According to the conservation of angular momentum, the initial angular momentum Li must equal the final angular momentum Lf:
Li=Iring⋅ω=mR2⋅ω
Lf=Itotal⋅ω′=3mR2⋅ω′
Setting these equal gives:
mR2⋅ω=3mR2⋅ω′
6. Solve for the Resultant Angular Velocity ω′:
Dividing both sides by mR2 (assuming m≠0 and R≠0):
ω=3ω′
Rearranging gives:
ω′=ω3
Final Result:
The resultant angular velocity ω′ of the ring after adding the two masses is:
ω′=ω3
We have a ring with an initial angular velocity ω and a mass m. Two additional masses, each of mass m, are placed at diametrically opposite points on the ring.
The moment of inertia I of a ring about its center is given by:
Iring=mR2
where R is the radius of the ring.
Each mass m is located at a distance R from the center of the ring. Since there are two masses, the total moment of inertia contributed by the two masses is:
Imasses=2⋅mR2=2mR2
The total moment of inertia Itotal of the system (ring + two masses) is:
Itotal=Iring+Imasses=mR2+2mR2=3mR2
According to the conservation of angular momentum, the initial angular momentum Li must equal the final angular momentum Lf:
Li=Iring⋅ω=mR2⋅ω
Lf=Itotal⋅ω′=3mR2⋅ω′
Setting these equal gives:
mR2⋅ω=3mR2⋅ω′
Dividing both sides by mR2 (assuming m≠0 and R≠0):
ω=3ω′
Rearranging gives:
ω′=ω3
The resultant angular velocity ω′ of the ring after adding the two masses is:
ω′=ω3
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A80videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B40videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions473videos
JEE MAIN
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question492videos
JEE MAIN 2022
Similar Questions
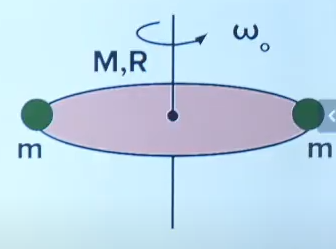
A thin circular right of mass M and radius R is rotating about its axis with an angular speed ω0 two particles each of mass m are now attached at diametrically opposite points. Find new angular speed of the ring.
View SolutionA disc of mass M and radius R is rotating about its axis with initial angular velocity of ω0 as shown. Now two small masses of m each one kept on the circumference diametrically opposite to eachother. Find new angular velocity
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
A(M+4mM)ωB(MM+4m)ωC(M+mM)ωD(MM+2m)ω - Question 2 - Select One
Initial angular velocity of a circular disc of mass M is ω1. Then two small spheres of mass m are attached gently to two diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc -
A(M+mM)ω1B(M+mm)ω1C(MM+4m)ω1D(MM+2m)ω1 - Question 3 - Select One
Initial angular velocity of a circualr disc of mass M is ω1. The tow sphere of mass ma re attached gently to diametrically opposite points ont eh edge of the disc. What is the final angular velocity on the disc?
A(M+mM)ω1B(M+mM)ω1C(MM+4m)ω1D(MM+2m)ω1
A thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its center and perpendicular to its plane with an angular velocity ω. Now two particles each of mass m are placed on its perimeter along a diameter along a diameter. Find the new angular velocity. If m=M/2, find the percentage change in the angular velocity.
View SolutionA thin circular ring of mass m and radius R is rotating about its axis with a constant angular velocity ω. Two objects each of mass M are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity ω'=
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with constant angular velocity ω . Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring . The ring now rotates with angular velocity given by
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity ω. The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
View SolutionA thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity ω. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
View Solution

