Four points lying on the curves form a square such that mid-points os sides also lies on the given curve. Find the square of area of the square
The correct Answer is:80
To solve the problem, we need to find the square of the area of a square formed by four points lying on the curve x2y2=1 such that the midpoints of the sides of the square also lie on the curve.
1. Understanding the Curve:
The equation x2y2=1 can be rewritten as xy=±1. This represents two rectangular hyperbolas: one in the first and third quadrants (where xy=1) and the other in the second and fourth quadrants (where xy=−1).
2. Identifying Points on the Curve:
Let the points on the curve be P(α,1α), Q(β,−1β), R(−α,−1α), and S(−β,1β). These points are symmetric about the origin.
3. Finding Midpoints:
The midpoints of the sides of the square can be calculated as follows:
- Midpoint of PQ: M1=⎛⎜⎝α+β2,1α−1β2⎞⎟⎠
- Midpoint of QR: M2=⎛⎜⎝−α−β2,−1α−1β2⎞⎟⎠
- Midpoint of RS: M3=⎛⎜⎝−α+β2,−1α+1β2⎞⎟⎠
- Midpoint of SP: M4=⎛⎜⎝α−β2,1α+1β2⎞⎟⎠
4. Condition for Midpoints:
Each midpoint must also satisfy the curve equation x2y2=1. Thus, we need to ensure that:
(α+β2)2⎛⎜⎝1α−1β2⎞⎟⎠2=1
5. Calculating Area:
The area A of the square can be calculated using the distance between two adjacent points (say P and Q):
A=OP⋅OQ=√α2+(1α)2⋅√β2+(−1β)2
Simplifying this gives:
A=√α2+1α2⋅√β2+1β2
6. Final Area Calculation:
The area of the square is 4A, and thus the square of the area is:
Area2=(4A)2=16A2
7. Substituting Values:
After substituting the values of α2 and β2 derived from the conditions, we find that the square of the area of the square is 80.
Final Answer:
The square of the area of the square is 80.
The equation x2y2=1 can be rewritten as xy=±1. This represents two rectangular hyperbolas: one in the first and third quadrants (where xy=1) and the other in the second and fourth quadrants (where xy=−1).
Let the points on the curve be P(α,1α), Q(β,−1β), R(−α,−1α), and S(−β,1β). These points are symmetric about the origin.
The midpoints of the sides of the square can be calculated as follows:
- Midpoint of PQ: M1=⎛⎜⎝α+β2,1α−1β2⎞⎟⎠
- Midpoint of QR: M2=⎛⎜⎝−α−β2,−1α−1β2⎞⎟⎠
- Midpoint of RS: M3=⎛⎜⎝−α+β2,−1α+1β2⎞⎟⎠
- Midpoint of SP: M4=⎛⎜⎝α−β2,1α+1β2⎞⎟⎠
Each midpoint must also satisfy the curve equation x2y2=1. Thus, we need to ensure that:
(α+β2)2⎛⎜⎝1α−1β2⎞⎟⎠2=1
The area A of the square can be calculated using the distance between two adjacent points (say P and Q):
A=OP⋅OQ=√α2+(1α)2⋅√β2+(−1β)2
Simplifying this gives:
A=√α2+1α2⋅√β2+1β2
The area of the square is 4A, and thus the square of the area is:
Area2=(4A)2=16A2
After substituting the values of α2 and β2 derived from the conditions, we find that the square of the area of the square is 80.
The square of the area of the square is 80.
Similar Questions
Knowledge Check
A side of a square is 16 cm. A new square is formed by joining the midpoints of sides, again a new square is formed by joining the mid-points of the new square and this process goes on till infiity. Find the total area of such square formed ?
A256cm2B128cm2C512cm2D1024cm2The length of side of a square is 'a' metre. A second square is formed by joining the middle points of this square. Then a third square is formed by joining the middle points of the sides of the second square and so on. Then, the sum of the areas of squares which carried upto infinity, is
Aa2B2a2C3a2D4a2
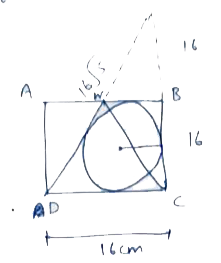
ABCD is a square . W is the mid point of AB side of square is 16 cm. Find the radius of circle in figure
View SolutionThe area of a square is 42.25 m2:
Find the side of the square.
View SolutionTwo squares have sides xcm and (x+4) . The sum of their areas is 656cm2 . Find the sides of the squares.
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View SolutionIf x and y are the sides of two squares such that y=x−x2. Find the change of the area of second square with respect to the area of the first square.
View SolutionIf sides of a square is (x+2y-z) units then the area of the square is.......
View Solution
