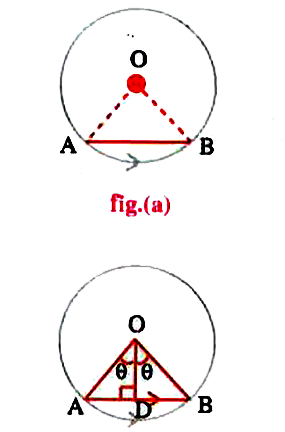
A particle travels from point A to B on a circular path of radius $15 / π c m$ . If the arc length AB be 10 cm , find the displacement (Figure)

Text Solution

Verified by Experts

Joining the initial (A) and final (B) positions of the body, the straight line AB is obtained which is its displacement (Figure)
We know ,
$\frac{Circumference}{arc length} = \frac{360^{\circ}}{Angle subtended by are at centre}$
$∴ \frac{2 π \times \frac{15}{π}}{10} = \frac{360^{\circ}}{20}$
$\Rightarrow 2 θ = 120^{\circ}$ . $\Rightarrow θ 60^{\circ}$
Now from right angle $Δ A D O$ ,
$A D = O A sin θ = (\frac{15}{π}) {sin 60}^{\circ} = \frac{15 \sqrt{3}}{2 π}$
$∴ A B = 2 A D = \frac{15 \sqrt{3}}{π} c m$ along A to B

Note,
Distance is scalar, but displacement is a vector quantiy.
Distance $\geq$ displacement
If a particle stars from a point and reaches the same point at the end of its journey, then displacement is zero. However distance covered is not zero .
The magnitude of displacement cannot exceed the distance of a particle in motion .

Updated on:21/07/2023

A particle travels from $A$ to $B$ path shown in figure, then the displacement of particle is :
.
A $2 \sqrt{2} m$
B $4 \sqrt{2} m$
C $52 m$
Dnone of these
A particle moves from A to B in a circular path of radius R covering an angle $θ$ as shown in figure. Find the ratio of magnitude of distance and magnitude of displacement of the particle.

A $\frac{θ}{2} . sin θ$
B $\frac{θ}{2 sin . \frac{θ}{2}}$
C $\frac{θ}{2 sin θ}$
D $\frac{θ}{sin . \frac{θ}{2}}$
A particle moves through angular displacement $θ$ on a circular path of radius' r'. The linear displacement will be:
A $2 r sin (\frac{θ}{2})$
B $2 r cos (\frac{θ}{2})$
C $2 r tan (\frac{θ}{2})$
D $2 r cot (\frac{θ}{2})$