For an ideal gas
a) The change in internal energy in a constant-pressure process from temperature T1 to T2 is equal to nCV(T2−T1), where CV is the molar heat capacity at constant volume and n is the number of moles of the gas
b) The change in internal energy of the gas and the work done by the gas are equal in magnitude in an adiabatic process
c) The internal energy does not change in an isothermal process
d) No heat is added or removed in an adiabatic process
Only a, b are correct
only b, d are correct
only c, d are correct
all are correct
The correct Answer is:D
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 1B
32 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 2
58 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - Problem
60 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
- THERMOMETRY BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11 Videos
Similar Questions
The molar heat capacity for an ideal monatomic gas is 3R.If dQ is the heat supplied to the gas and dU is the change in its internal energy then for the process the ratio of work done by the gas and heat supplied is equal to
View SolutionStatement-1 : In an adiabatic process, change in internal energy of a gas is equal to work done on/by the gas in the process.
Statement-2 : This is because temp.of gas remains constant in an adiabatic process.
View Solution
Knowledge Check
For an ideal gas,
(i) the change in internal energy in a constant pressure process from temperature T1 to T2 is equal to nCV(T2−T1), where CV is the molar heat capacity at constant volume and n is the number of moles of the gas
(ii) The change in internal enregy of the gas and the work done by the gas are equal in magnitude in an adiabatic process.
(iii) The internal energy does not change in an isothermal process. ltbr> (iv) no heat is added or removed in an adiabatic processA(i),(iii)B(ii),(iii)C(iii),(iv)DallThe molar heat capacity of a gas at constant volumes is CV. If n moles of the gas under ΔT change in temperature it's internal energy will change by nCVΔT
Aonly if the change of temperature occurs at constant volumeBonly if the change of temperature occurs at constant pressureCin any process which is not adiabaticDin any processThe temperature of 2 moles of a gas is changed from 20∘C to 30∘C when heated at constant volume. If the molar heat capacity at constant volume is 8 J mol−1K−1, the change in internal energy is
A80 JB20 JC160 JD16 J
V-T graph of a process of monoatomic ideal gas is shown in figure.
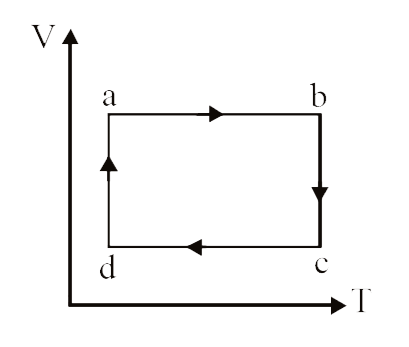
Change in internal energy of the gas is zero in process(s)-
View SolutionOne mole of an ideal gas goes through a process in which the entropy of the gas changes with temperature T as S=aT+CV1nT, where a is a positive constant. CV is the molar heat capacity of this gas at constant volume. Find the volume dependence of the gas temperature in this process if T=T0 at V=V0.
View SolutionAssertion : In an adiabatic process, change in internal energy of a gas is equal to work done on/by the gas in the process.
Reason : This is because temp.of gas remains constant in an adiabatic process.
View SolutionStatement-1 : In an adiabatic process, change in internal energy of a gas is equal to work done on/by the gas in the process.
Statement-2 : This is because temp.of gas remains constant in an adiabatic process.
View SolutionA monoatomic gas of n-moles is heated temperature T1 to T2 under two different conditions
(i) at constant volume and
(ii) At constant pressure The change in internal energy of the gas is
View Solution
