A square surface of side L metres is in the plane of the paper. A unif

Class 12 PHYSICS ELECTROSTATICS

Knowledge Check

A square surface of side $L m$ is in the plane of the paper. A uniform electric field $\to E (V / m)$ , also in the plane of the paper, is limited only to the lower half of the square surface (see figure). The electric flux in $S I$ units associated with the surface is:

A $E L^{2} / (2 ε_{0})$
B $E L^{2} / 2$
Czero
D $E L^{2}$
Answer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
$ϕ_{E} = \int \to E . \to d s$ , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface $\oint E = \oint \to E . \to d s .$ it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by $\in_{0} .$ Mathematically $\oint \to E . \to d s = \frac{1}{\in_{0}} [q_{e n}]$ , where $q_{c n}$ is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
A square surface of side L m is in the plane of paper. A uniform electric field $\to E V m^{- 1}$ , also in the plane of the paper, is limited only to the lower half of the square surface as shown in adjoining figure. The electric flux, in SI units, associated with the surfer is :
(##U_LIK_SP_PHY_XII_C01_E03_012_Q01.png" width="80%">
Azero
B $E L^{2}$
C $\frac{E L^{2}}{2 \in_{0}}$
D $\frac{E L^{2}}{2}$
A square surface of side $L$ metre in the plane of the paper is placed in a uniform electric field $E (volt / m)$ acting along the same place at an anlge $θ$ with the horizontal side of the square as shown in figure. The electric flux linked to the surface in uint of $V - m$ is

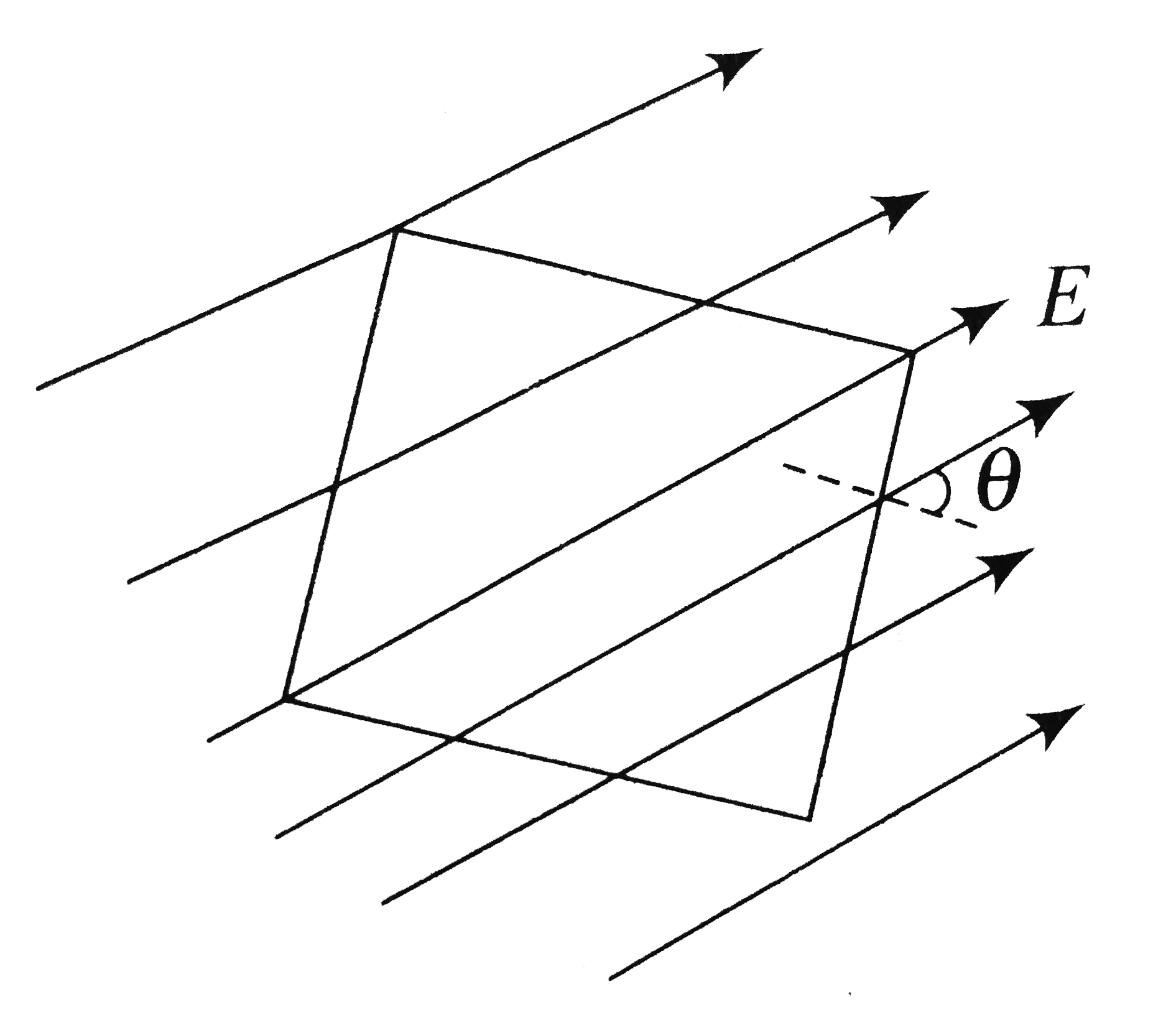A $E L^{2}$
B $E L^{2} cos θ$
C $E L^{2} sin θ$
D0

A square surface of side L metres is in the plane of the paper. A uniform electric field $\to E$ (volt/m), also in the plane of the paper, is limited only to lower half of the square surface. The electric flux in SI units associated with the surface is

The correct Answer is:D

Similar Questions

Knowledge Check

A square surface of side $L m$ is in the plane of the paper. A uniform electric field $\to E (V / m)$ , also in the plane of the paper, is limited only to the lower half of the square surface (see figure). The electric flux in $S I$ units associated with the surface is:

A square surface of side $L$ metre in the plane of the paper is placed in a uniform electric field $E (volt / m)$ acting along the same place at an anlge $θ$ with the horizontal side of the square as shown in figure. The electric flux linked to the surface in uint of $V - m$ is

Recommended Questions

A square surface of side L metres is in the plane of the paper. A uniform electric field →E(volt/m), also in the plane of the paper, is limited only to lower half of the square surface. The electric flux in SI units associated with the surface is

The correct Answer is:D

Similar Questions

Knowledge Check

A square surface of side Lm is in the plane of the paper. A uniform electric field →E(V/m), also in the plane of the paper, is limited only to the lower half of the square surface (see figure). The electric flux in SI units associated with the surface is:

A square surface of side L metre in the plane of the paper is placed in a uniform electric field E(volt/m) acting along the same place at an anlge θ with the horizontal side of the square as shown in figure. The electric flux linked to the surface in uint of V−m is

Recommended Questions

A square surface of side L metres is in the plane of the paper. A uniform electric field $\to E$ (volt/m), also in the plane of the paper, is limited only to lower half of the square surface. The electric flux in SI units associated with the surface is

A square surface of side $L m$ is in the plane of the paper. A uniform electric field $\to E (V / m)$ , also in the plane of the paper, is limited only to the lower half of the square surface (see figure). The electric flux in $S I$ units associated with the surface is:

A square surface of side $L$ metre in the plane of the paper is placed in a uniform electric field $E (volt / m)$ acting along the same place at an anlge $θ$ with the horizontal side of the square as shown in figure. The electric flux linked to the surface in uint of $V - m$ is