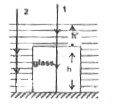
Two beams of light are incident normally on water (μ = 4/3). If one of the beams passes through a glass (μ = 3/2) slab of height 'h' has shown in the figure, the time difference for both the beams for reaching the bottom is (C is velocity of light is vacuum)

zero
h3C
6hC
h6C
The correct Answer is:D
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS))
9 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
2 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))
17 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
98 Videos
Similar Questions
Two beams of light are incident normally on water (R.l. = 43). If the beam 1 passes through a glass (R.l. = 32) slab of height h as shown in the figure, the time difference for both beams for reaching the bottom is
View SolutionA ray of light passes normally through a slab (μ=1.5) of thickness t. If the speed of light in vacuum be C, then time taken by the ray to go across the slab will be
View Solution
Knowledge Check
Two beams of light are incident normally on water (R.l. = 43). If the beam 1 passes through a glass (R.l. = 32) slab of height h as shown in the figure, the time difference for both beams for reaching the bottom is
 AzeroBh′6CC6hCDh6C
AzeroBh′6CC6hCDh6CTwo beams of light are incident normally on water (R.l. = 43). If the beam 1 passes through a glass (R.l. = 32) slab of height h as shown in the figure, the time difference for both beams for reaching the bottom is
 AZeroBh6CC6hCDh6C
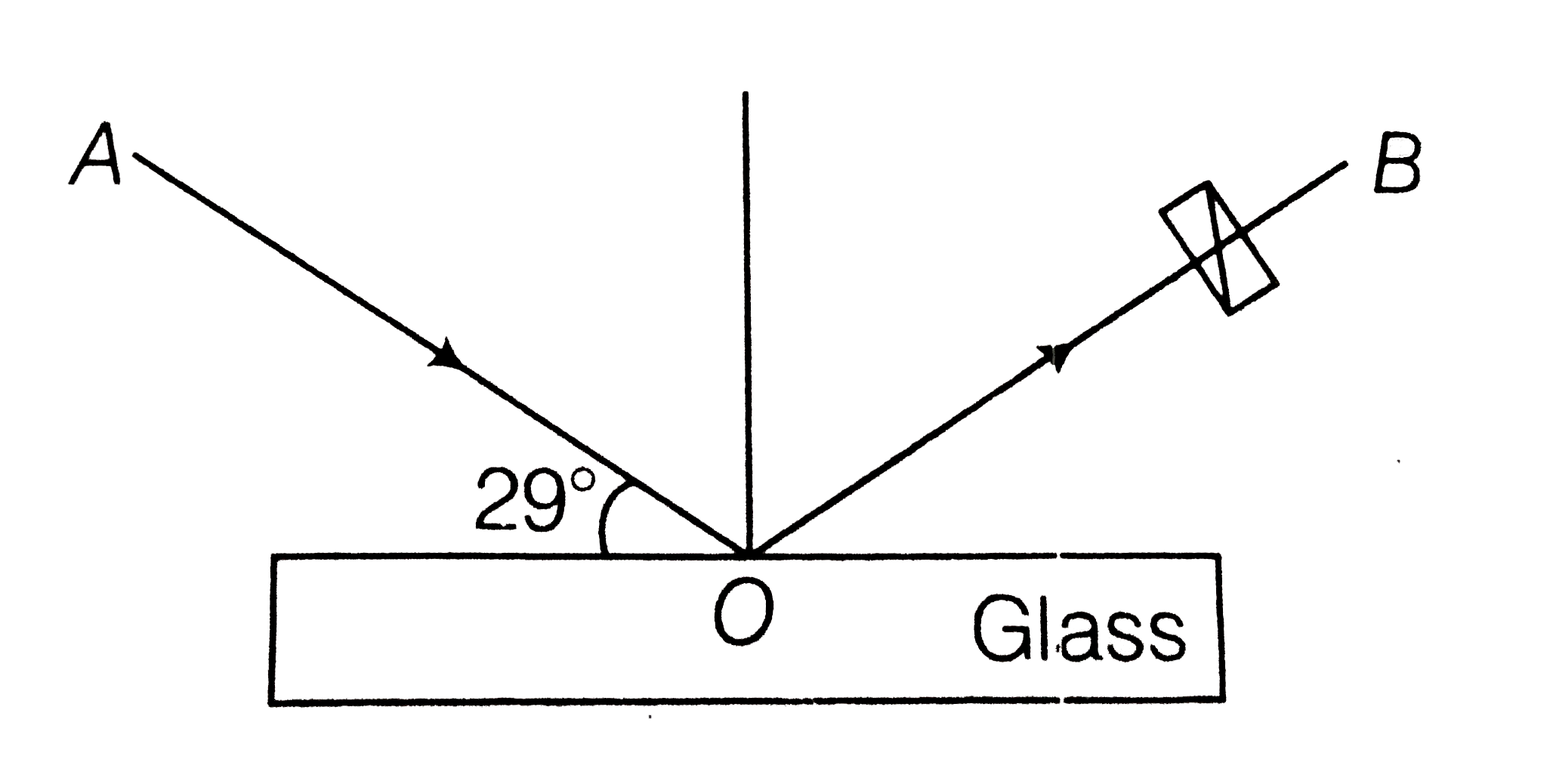
AZeroBh6CC6hCDh6CA beam of light AO is incident a glass slab (μ=1.54) in the direction show. The reflected ray OB is passed through a Nicol prism. On viewing through a Nicol prism, we find on rotating the prism that
 Athe intensity is reduceed down to zero and remains zeroBthe intensity reducees down somewhat and rises againCthere is no change in intensityDthe intensity gradually reduces to zero and then again increases
Athe intensity is reduceed down to zero and remains zeroBthe intensity reducees down somewhat and rises againCthere is no change in intensityDthe intensity gradually reduces to zero and then again increases
A light beam is incident on a rectangular glass plate (μ=1.54) The reflected light OB passes through a nicol prism.
On observing the transmitted light while rotating the prism, it is seen that
View SolutionQ."4 A light ray travels in a glass slab of refractive index μ=2 .Find the time taken by the light ray to travel in the glass slab for a distance of 20√3d(Velocity of light =c )
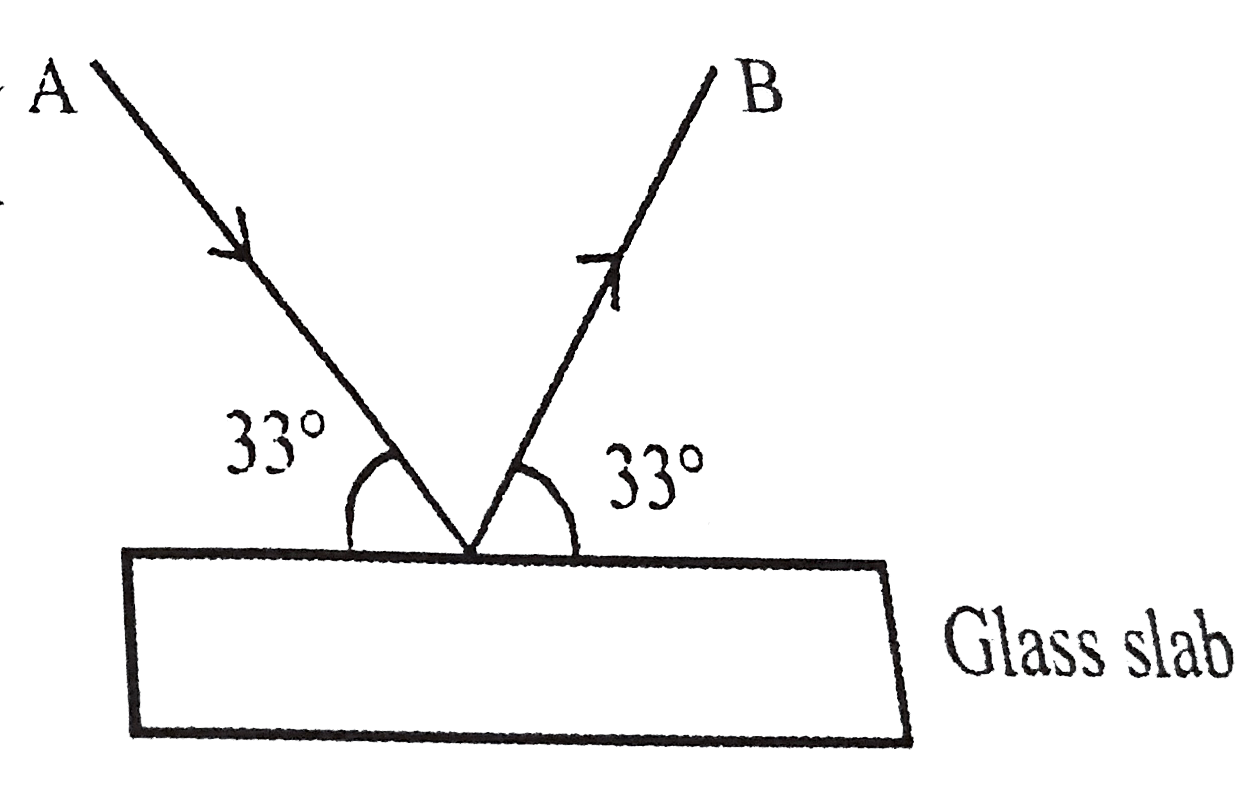
View SolutionA beam of light is incident on a glass slab (μ=1.54) in a direction as shown in the figure. The reflected light is analysed by a polaroid prism. On rotating the polaroid, (tan57∘=1.54)
View SolutionLight passes through a rectangular glass slab and through a triangular glass prism. In what way does the direction of the two emergent beams differ and why?
View SolutionA beam of light falls on a glass plate (μ=3/2) of thickness 6.0 cm at an angle of 60∘. Find the deflection of the beam on passing through the plate. (in cm).
View Solution
