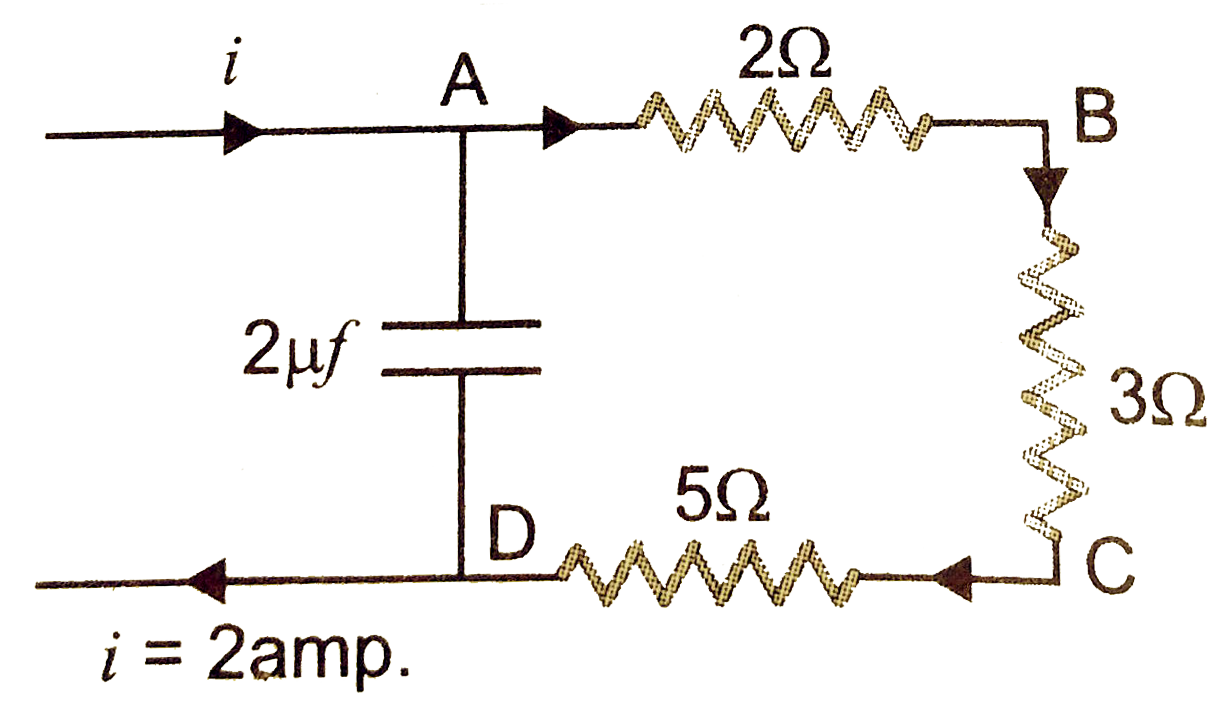An inductor of inductance L and resistance R has energy stored E in it in the discharging LR circuit the time after which energy stored will be 25% of initial energy is
LR
Lln2R
L2R
Lln(2)2R
To solve the problem of finding the time after which the energy stored in an inductor in an LR circuit is 25% of its initial energy, we can follow these steps:
Step 1: Understand the initial energy stored in the inductor
The energy stored in an inductor E is given by the formula:
E=12LI2
where L is the inductance and I is the current flowing through the inductor.
Step 2: Determine the initial current
At t=0, the current I0 through the inductor can be expressed as:
I0=VR
where V is the voltage across the inductor and R is the resistance.
Step 3: Calculate the initial energy stored
Substituting I0 into the energy formula, the initial energy E0 stored in the inductor is:
E0=12LI20=12L(VR)2
Step 4: Express the energy at time t
At any time t, the current I(t) in the discharging LR circuit can be expressed as:
I(t)=I0e−RLt
Thus, the energy stored at time t is:
E(t)=12L(I(t))2=12L(I0e−RLt)2=12LI20e−2RLt
Step 5: Set up the equation for 25% of initial energy
We want to find the time t when the energy stored is 25% of the initial energy:
E(t)=14E0
Substituting the expressions for E(t) and E0:
12LI20e−2RLt=14(12LI20)
Step 6: Simplify the equation
Canceling 12LI20 from both sides gives:
e−2RLt=14
Step 7: Take the natural logarithm
Taking the natural logarithm of both sides:
−2RLt=ln(14)
Since ln(14)=−ln(4)=−2ln(2), we can rewrite the equation as:
−2RLt=−2ln(2)
Step 8: Solve for t
Now, solving for t:
t=LRln(2)
Final Answer
Thus, the time after which the energy stored will be 25% of the initial energy is:
t=LRln(2)
---
The energy stored in an inductor E is given by the formula:
E=12LI2
where L is the inductance and I is the current flowing through the inductor.
At t=0, the current I0 through the inductor can be expressed as:
I0=VR
where V is the voltage across the inductor and R is the resistance.
Substituting I0 into the energy formula, the initial energy E0 stored in the inductor is:
E0=12LI20=12L(VR)2
At any time t, the current I(t) in the discharging LR circuit can be expressed as:
I(t)=I0e−RLt
Thus, the energy stored at time t is:
E(t)=12L(I(t))2=12L(I0e−RLt)2=12LI20e−2RLt
We want to find the time t when the energy stored is 25% of the initial energy:
E(t)=14E0
Substituting the expressions for E(t) and E0:
12LI20e−2RLt=14(12LI20)
Canceling 12LI20 from both sides gives:
e−2RLt=14
Taking the natural logarithm of both sides:
−2RLt=ln(14)
Since ln(14)=−ln(4)=−2ln(2), we can rewrite the equation as:
−2RLt=−2ln(2)
Now, solving for t:
t=LRln(2)
Thus, the time after which the energy stored will be 25% of the initial energy is:
t=LRln(2)
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A80videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B40videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions473videos
JEE MAIN
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question492videos
JEE MAIN 2022
Similar Questions
Knowledge Check
- Question 1 - Select One
In a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
A(ln2)LRB0.5LRC√2LRD(√2√2−1)LR - Question 2 - Select One
An inductance L and a resistance R are connected in series with a battery of emf ε. The maximum rate at which the energy is stored in the magnetic field is :
Aε4RBε2RC2RεD4Rε - Question 3 - Select One
An inductance L and a resistance R are connected in series with a battery of emf ε. The maximum rate at which the energy is stored in the magnetic field is :
Aε4RBε2RC2RεD4Rε
For a circuit arrangement shown in figure, energy stored will be
 View Solution
View SolutionFind total energy stored in capacitors given in the circuit.
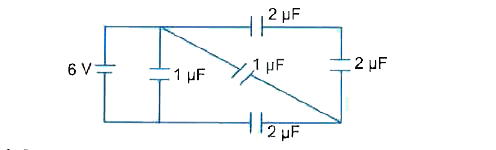 View Solution
View SolutionEnergy Stored In An Inductor
View SolutionFind total energy stored in capacitors given in the circuit
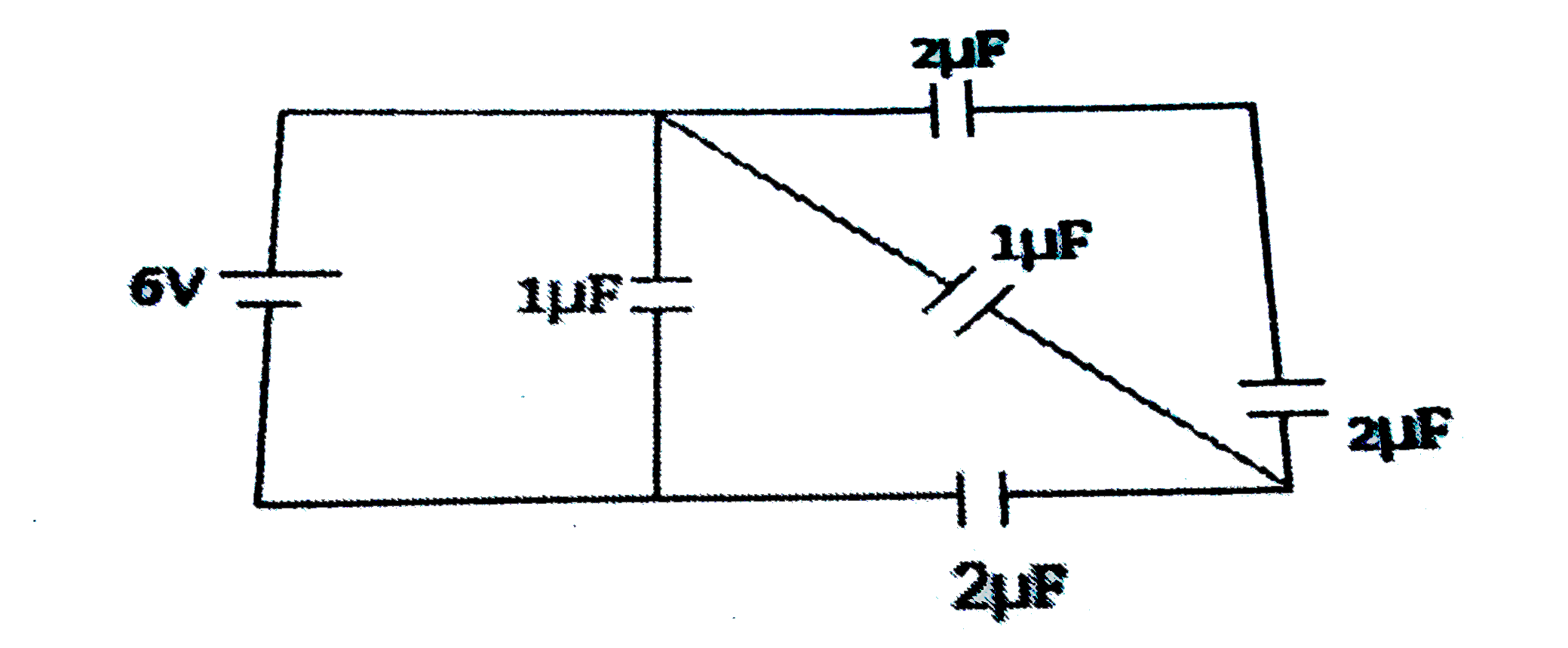 View Solution
View SolutionIn an inductor of inductance L=100mH, a current of I=10A is flowing. The energy stored in the inductor is
View Solution