The correct Answer is:A, B, C
Topper's Solved these Questions
- INDEFENITE & DEFINITE INTEGRATION BOOK - BANSAL HINDICHAPTER - INDEFENITE & DEFINITE INTEGRATION EXERCISE - SECTION -B [DEFINITE INTEGRATION] (SPECIAL DPP-2)
23 Videos
- INDEFENITE & DEFINITE INTEGRATION BOOK - BANSAL HINDICHAPTER - INDEFENITE & DEFINITE INTEGRATION EXERCISE - SECTION -B [DEFINITE INTEGRATION] (SPECIAL DPP-3)
12 Videos
- INDEFENITE & DEFINITE INTEGRATION BOOK - BANSAL HINDICHAPTER - INDEFENITE & DEFINITE INTEGRATION EXERCISE - EXERCISE-I (SPECIAL DPP 4) SECTION -A ( INDEFINITE INTEGRATION ) SPECIAL DPP-IV
15 Videos
- DETERMINANT & MATRICSBOOK - BANSAL HINDICHAPTER - DETERMINANT & MATRICSEXERCISE - EXERCISE -5 (RANK BOOSTER)
15 Videos
- INVERSE TRIGNOMETRIC FUNCTIONSBOOK - BANSAL HINDICHAPTER - INVERSE TRIGNOMETRIC FUNCTIONSEXERCISE - EXERCISE-5 (RANK BOOSTER)
10 Videos
Similar Questions
निम्न निश्चित समाकलन का मान ज्ञात कीजिए।
1∫0dxx2+2xcosα+1 जहाँ −π<α<π
View Solutionπ/2∫0(xcosx+1)esinxdxπ/2∫0(xsinx−1)ecosxdx का निरपेक्ष मान होगा।
View Solutionसमाकलन ज्ञात कीजिए।
∫logxx3dx
View Solutionमाना f(x)=∣∣ ∣ ∣∣sinxsin(x+h)sin(x+2h)sin(x+2h)sinxsin(x+h)sin(x+h)sin(x+2h)sinx∣∣ ∣ ∣∣ है। यदि Limh→0f(x)h2 का मान k(sinx+sin3x)हो , तो प्राकृत संख्या k का मान ज्ञात कीजिये।
View Solutionनिम्नलिखित फलन का प्रान्त व परिसर ज्ञात करो।
f(x)=cos−1(√2x2+1x2+1),
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
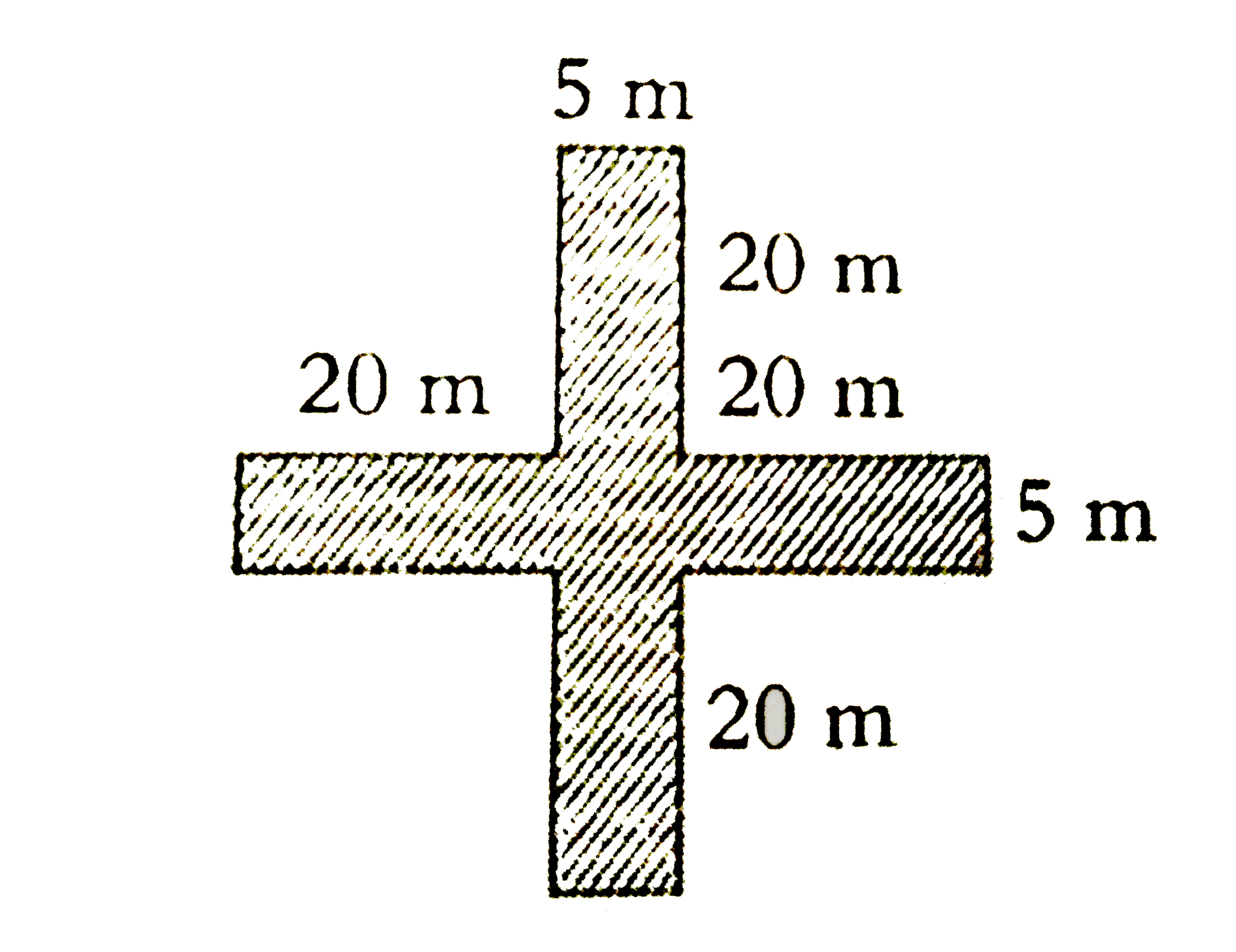
View SolutionThe area of the shaded part in the figure given below is ______.
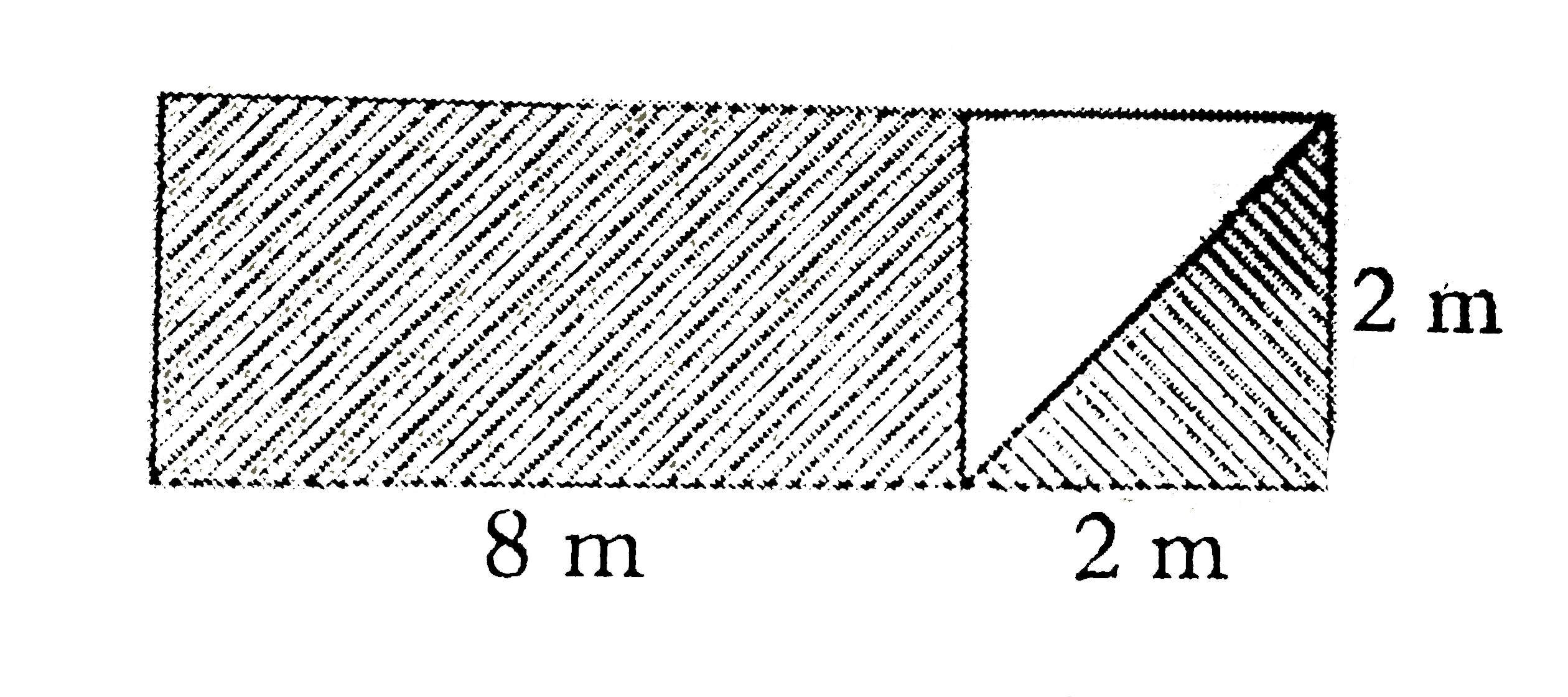
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution

