A particle moves along a straight line according to the equation s = 8 cos 2t + 4sint. The initial velocity is Solution in Telugu
−5 units/sec
−4 units/sec
23e units/sec
5 units/sec
The correct Answer is:C
Step by step video, text & image solution for A particle moves along a straight line according to the equation s = 8 cos 2t + 4sint. The initial velocity is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - RATE MEASUREMENTEXERCISE - PRACTICE SHEET (EXERCISE - 1) (LEVEL - 1) (STRAIGHT OBJECTIVE TYPE QUESTION)43videos
RATE MEASUREMENT
- BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES55videos
PROPERTIES OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - RATE OF CHANGEEXERCISE - Advanced Subjective Type Questions22videos
RATE OF CHANGE
Similar Questions
If a particle moves alonga straight line by S=4t2−8t+3 and the time at which the particle comes of rest is 't' seconds then '2t' is
01:46View SolutionIf ¯¯¯¯¯¯OA=¯i+2¯j−3¯k,¯¯¯¯¯¯OB=3¯i−2¯j+5¯kand2¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB then ¯¯¯¯¯¯AC=
05:34View SolutionA stone is dropped into a quiet pond and waves move in circles outward from the place where it strikes, at a speed of 30 cm per second. At the instant when the radius of the wave ring is 50 mt, find the rate of increase in the area and in the circumference of the wave ring.
04:48View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity? .
01:54View SolutionA particle is moving in a straight line as : a=1m//s^(2) 0letle10 a=2t tgt10 where t is the time and a is the acceleration. If initial velocity of the particla is zero then :
01:43View SolutionAcceleration vs time graph for a particle moving along a straight line is as shown. If the initial velocity of the particle is u=10m/s, draw a plot of its velocity vs time for 0<t<8.
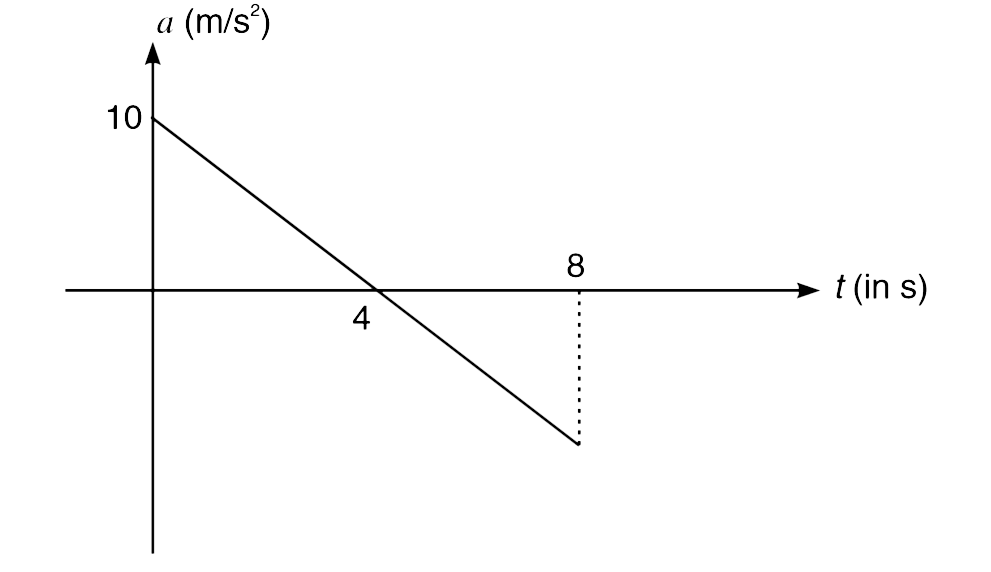 01:50View Solution
01:50View SolutionA particle moving in a straight in a straight line has velocity and displacement equation as v = 4 sqrt(1 + s) , where v is in m/s and s is in m. The initial velocity of the particle is:
03:11View SolutionA particle moves along a straight line according to the law s=16−2t+3t3, where s metres is the distance of the particle from a fixed point at the end of t second. The acceleration of the particle at the end of 2s is
01:22View SolutionPosition of a particle moving along a straight line is given by x=2t^(2)+t . Find the velocity at t = 2 sec.
01:22View SolutionA particle moves along a line according to the law s=t4−5t2+8. The intial velocity is
09:12View Solution[" A particle is moving along "],[" a straight line with non- "],[" uniform acceleration.The "],[" displacement of the "],[" particle is given by "],[S=2t^(3)+3t^(2)+5t" where "S" is in "],[" metres and "t" is in seconds."],[" The velocity of the particle "],[" at "t=2" seconds is "]
04:25View Solution[" A particle is moving along "],[" a straight line with non- "],[" uniform acceleration.The "],[" displacement of the "],[" particle is given by "],[S=2t^(3)+3t^(2)+5t" where "S" is in "],[" metres and "t" is in seconds."],[" The velocity of the particle "],[" at "t=2" seconds is "]
02:37View SolutionThe acceleration time graph of a particle moving along a straight line is as shown. The time at which the particle will have the velocity same as initial velocity (in s) is?
02:37View SolutionThe displacement of a particle moving along a straight line is given by
s=3t^(3)+2t^(2)-10t. find initial velocity and acceleration of particle.08:16View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
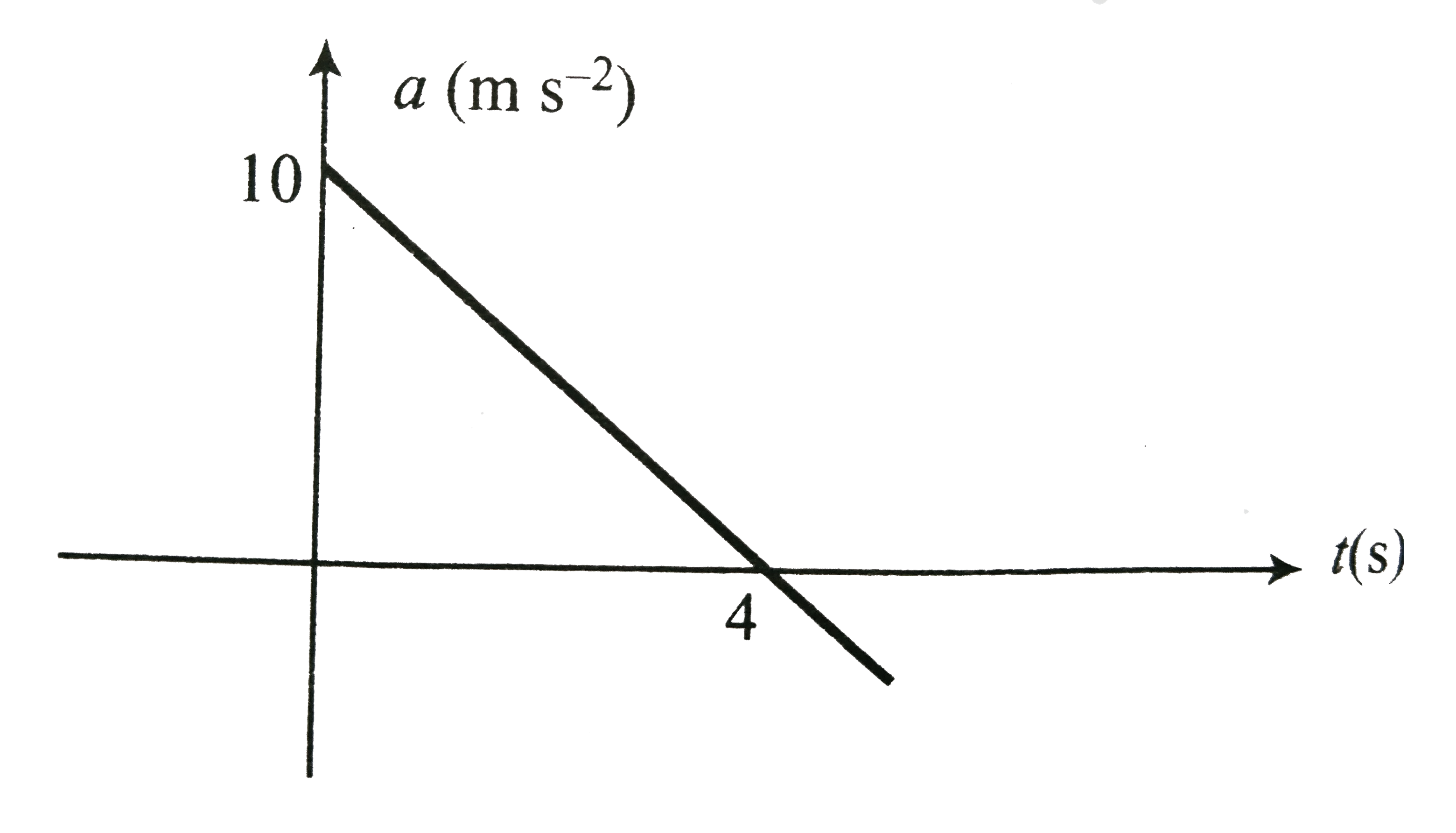 .03:20View Solution
.03:20View Solution

