f(x) is continous and differentiable function .Given , f(x) assumes valus of the form ±√I where I denotes set of whole numbers whenever x=a or b , otherwise f(x) assumes real values. Also , f(c)=−32and|f(a)|≤|f(b)|
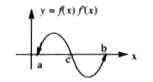
f(x) is continous and differentiable function .Given , f(x) assumes valus of the form +-sqrt(I) where I denotes set of whole numbers whenever x=a or b , otherwise f(x) assumes real values. Also , f(c)=-(3)/(2)and|f(a)|le|f(b)| The number of rational values that f(a) +f(b)+f(c ) can assume is /are
The number of rational values that f(a) +f(b)+f(c ) can assume is /are

A

4

B

2

C

3

D

5

Text Solution
Verified by Experts

The correct Answer is:C

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 11MATHSMAXIMA AND MINIMA

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If f (x) is continous on [0,2], differentiable in (0,2)f(0)=2,f(2)=8andf'(x)≤3 for all x in (0,2), then find the value of f (1).

    A4
    B5
    C6
    D7

  • Given that f is a real valued differentiable function such that f(x)f'(x)<0 for all real x, it follows that

    Af(x) is an increasing function
    Bf(x) is a decreasing function
    C|f(x)| is an increasing function
    D|f(x)| is a decreasing function

  • Let f (x) is continuous on [a,c] and differentiable in (a,c) where a,b,c are real numbers : a<b<c.Iff'(x) is strictly increasing function and
    (c−b)f(a)+(b−a)f(c)=k, then

    Ak>(c−a)f(b)
    Bk<(c−a)f(b)
    Ck=(c−a)f(b)
    Dk≤2(c−a)f(b)