The function $f (x) = \sqrt{(a x^{3} + b x^{2} + c x + d)}$ has its nonzero local minimum an d maximum values at x=-2 andx=2 , repectively . If a is a root of $x^{2} - x - x 6 = 0$ , then match the following

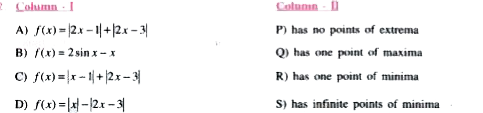
Text Solution

Verified by Experts

The correct Answer is:A-s;B-s;C-r;D-q

Updated on:21/07/2023

|

Class 11 MATHS MAXIMA AND MINIMA

Topper's Solved these Questions

MAXIMA AND MINIMA BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (LINKED COMPREHENSION TYPE QUESTIONS)
6 Videos
MAXIMA AND MINIMA BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (INTEGER TYPE QUESTIONS)
3 Videos
MAXIMA AND MINIMA BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
10 Videos
MAXIMA & MINIMABOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III
35 Videos
MEAN VALUE THEOREMSBOOK - AAKASH SERIESCHAPTER - MEAN VALUE THEOREMSEXERCISE - PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )
2 Videos

Similar Questions

Knowledge Check

The function $f (x) = 2 x^{3} - 3 (a + b) x^{2} + 6 a b x$ has a local maximum at $x = a$ , if
A $a > b$
B $a < b$
C $a > 0$
D $a < 0$
The condition that f(x)= $a x^{3} + b x^{2} + c x + d$ has no extreme value is
A $b^{2} > 3 a c$
B $b^{2} = 4 a c$
C $b^{2} = 3 a c$
D $b^{2} < 3 a c$
The function $f (x) = \frac{x}{2} + \frac{2}{x}$ has a local minimum at $x = 2$ (b) $x = - 2$ $x = 0$ (d) $x = 1$
A $x = 2$
B $x = - 2$
C $x = 0$
D $x = 1$

AAKASH SERIES-MAXIMA AND MINIMA -ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MATRIX MATCHING TYPE QUESTIONS)

Home
Ask Doubt
Profile