Suppose you do not know the function f(x) , however some information about f(x) is listed below. Read the following carefully before attempting the questions
(i) f(x) is continuous and defined for all real numbers
(ii) f'(-5)=0 , f'(2) is not defined and f'(4)=0
(iii) (-5,12) is a point which lies on the graph of f(x)
(iv) f"(2) is undefined , but f"(x) is negative everywhere else.
(v) the signs of f(x) is given below
Suppose you do not know the function f(x) , however some information about f(x) is listed below. Read the following carefully before attempting the questions (i) f(x) is continuous and defined for all real numbers (ii) f'(-5)=0 , f'(2) is not defined and f'(4)=0 (iii) (-5,12) is a point which lies on the graph of f(x) (iv) f
From the possible graph of y=f(x) , we can say that

A

There is exactly one point of inflection on the curve.

B

f(x) increases on −5<x<2andx>4 and decreases on
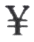
ocr_image
<x<−5and2<x<4.

C

The curve is always concave down.

D

Curve always concave up.

Text Solution
Verified by Experts

The correct Answer is:C

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 11MATHSMAXIMA AND MINIMA

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Column AA function f(x) is defined for all real numbers asColumn Bf(x)=(x−1)(x−2)(x−3)(x−4)f(2.5)f(3.5)

    AIf column A is larger
    BIf column B is larger
    CIf the columns are equal
    DIf there is not enough information to decide