एक कण xy-तल में समीकरण x=αt तथा y=αt(1−βt) के अनुसार गतिमान है, जहाँ α तथा β धनात्मक अचर है तथा t समय है :
कण के पथ का समीकरण है -
y=x(1−αβx)
y=x(1−βαx)
y=αx(1−βx)
y=βx(1−αx)
The correct Answer is:B
दोंनो समीकरण से .t. हटाने पर-
⇒t=xα⇒y=x(1−βαx)
Topper's Solved these Questions
Similar Questions
एक कण A को चाल VA से, क्षैतिज से 60° का कोण बनाते हुए किसी बिन्दु से प्रक्षेपित किया जाता है। उसी क्षण पर वेग VB से, द्वितीय कण B (समान क्षैतिज तल में) को ऊर्ध्व ऊपर की ओर उस बिन्दु से फेंका जाता है जो A कण के परवलयाकार पथ के अधिकतम ऊँचाई वाले बिन्दु के ठीक नीचे है। अगर दोंनो कण टकराते है तो VA/VB का अनुपात होगा-
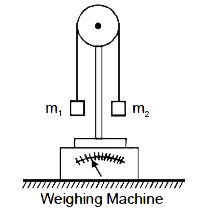
03:10View Solutionएक हल्की रस्सी से जुड़े दो द्रव्यमान m1 तथा m2 घर्षण रहित घिरनी पर रखे है। द ये अनुसार इस प्रक्रम को एक भार तुला पर रखा है। m1 तथा m2 के तीन संयोजनों का उपयोग किया जाता है, प्रथम संयोजन में m1=6 किग्रा. तथा m2=2 किग्रा., द्वितीय संयोजन में m1=5 किग्रा. तथा m2=3किग्रा. तथा तीसरे संयोजन में m1=4 किग्रा. तथा m2=4 किग्रा. है। प्रारम्भ में द्रव्यमानों को स्थिर पकड़कर मुक्त रूप से छोड़ा जाता है। मुक्त करने के प चात् तीनों संयोजनों में यदि __ भार तुला के पाठ्यांक क्रम :W1W2 तथा W3 हों तो -
 07:05View Solution
07:05View Solutionएक रेखा के कार्तीय समीकरण 6x−2=3y+1=2z−2 है। रेखा के दिक्-अनुपात ज्ञात कीजिए तथा बिन्दु (2,−1,−1) से गुजरने वाली उस रेखा का सदिश समीकरण लिखिए जो दी हुई रेखा के समान्तर है।
04:52View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
03:29View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओ के समीकरणy=ax,y=bx तथा ax+by+c=0 है
03:14View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
05:29View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
03:23View Solutionमाना की α,β समीकरण px2+qx+r=0,p≠0 के मूल है | यदि p,q,r समान्तर श्रेणी में हों तथा 1α+1β=4 तो | α−β | का मात्र है :
02:05View Solutionएक परवलय के नाभिलम्ब का समीकरण x+y=8 तथा उसके शीर्ष पर स्पर्शी का समीकरण x+y=12 है, तो उसके नाभिलम्ब की लम्बाई है :
04:35View Solutionएक कण y=x2+2x से साथ-साथ चलता है। व्रक के किस बिंदु पर x तथा y निर्देशांक समान दर से परिवर्तित हो रहे है ?
05:00View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
04:10View Solutionयदि समीकरण x2−2x+2=0 के मूल α तथा β हैं, तो n का न्यूनतम मान, जिसके लिए (αβ)n=1 है
02:16View Solutionमाना a, b तथा c एक समांतर श्रेढ़ी (जोकि अचर समांतर श्रेढ़ी नहीं है) के क्रमश: 7 वे तथा 11 वे, 13 वे पद है। यदि ये एक गुणेत्तर श्रेढ़ी के भी तीन क्रमागत पद है, तो ac बराबर है
02:32View Solutionयदि α=(λ−2)a+b तथा β=(4λ−2)a+3b दो दिए गए सदिश है, जहाँ सदिश a तथा b सरीख नहीं है । λ का वह मान जिसके लिए α तथा β सरीख है, है
02:36View Solutionउस सरल रेखा का समीकरण जो बिन्दु (1,-2) से गुजरती है तथा रेखा 3x-5y+7=0 के लम्बवत है, है
02:47View Solutionउस सरल रेखा का समीकरण जो रेखाओं 3x-y+ 2 = 0 तथा 5x-2y+ 7 = 0 के प्रतिच्छेद बिन्दु से गुजरती है तथा जिसकी प्रवणता अनन्त है, होगा
03:06View Solution

