एक बिंदु P से वृत्त x2+y2−2x−4y+4=0 पर दो स्पर्श रेखाएँ खींची गई हैं। इन स्पर्श रेखाओं के बीच का कोण tan−1(125) है, जहाँ tan−1(125)∈(0,π) है। यदि वृत्त का केन्द्र C है तथा ये स्पर्श रेखाएँ वृत्त को बिंदुओं A तथा B पर स्पर्श करती हैं, तो ΔPAB तथा ΔCAB के क्षेत्रफलों का अनुपात है :
11:4
3:1
9:4
2:1
Step by step video & image solution for एक बिंदु P से वृत्त x^(2)+y^(2)-2x-4y+4=0 पर दो स्पर्श रेखाएँ खींची गई हैं। इन स्पर्श रेखाओं के बीच का कोण tan^(-1)((12)/(5)) है, जहाँ tan^(-1)((12)/(5)) in (0,pi) है। यदि वृत्त का केन्द्र C है तथा ये स्पर्श रेखाएँ वृत्त को बिंदुओं A तथा B पर स्पर्श करती हैं, तो DeltaPAB तथा DeltaCAB के क्षेत्रफलों का अनुपात है : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सॉल्वड पेपर्स 2021BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2021EXERCISE - Mathematics (Section B )
10 Videos
- सॉल्वड पेपर्स 2021BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2021EXERCISE - MATHEMATICS (SECTION A)
38 Videos
- सॉल्वड पेपर्स 2021BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2021EXERCISE - MATHEMATICS SECTION B
20 Videos
- सॉल्वड पेपर्स 2020BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2020EXERCISE - MATHEMATICS
36 Videos
- स्पर्शी एवं अभिलम्ब BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्पर्शी एवं अभिलम्ब EXERCISE - एकल पूर्णांक प्रश्न
1 Videos
Similar Questions
3n संख्याओं का एक समुच्चय है, जिसका प्रसरण 4 है। इस समुच्चय में, प्रथम 2n संख्याओं का माध्य 6 है तथा शेष n संख्याओं का माध्य 3 है। प्रथम 2n संख्याओं में प्रत्येक में 1 जोड़ कर तथा शेष n संख्याओं में प्रत्येक से 1 घटा कर एक नया समुच्चय बनाया गया है। यदि नये समुचय का प्रसरण k है, तो 9k बराबर है ________।
View Solutionमाना g(x)=∫x0f(t)dt, जहाँ [0,3] में f एक संतत फलां है, 13≤f(t)≤1∀t∈[0,1] है तथा 0≤f(t)≤12∀t∈(1,3] है| अधिकतम सम्भव अंतराल, जिसमे g(3) स्तिथ है, है|
View Solutionमाना p=⎡⎢⎣−302056901401121206014⎤⎥⎦ तथा A=⎡⎢⎣27ω2−1−ω10−ω−ω⎤⎥⎦ हैं, जहाँ ω=−1+i√32 है तथा 3 कोटि का तत्समक आव्यूह I3 है। यदि आव्यूह (P−1AP−I3)2 का सारणिक αω2 है, तो x का मान बराबर है ________
View Solutionमान लीजिये कि a, b द्विघातीय बहुपद (quadratic polynomial) x2+20x−2020 के भिन्न वास्तविक मूलों (distinct real roots) को दशति हैं, एवं मान लीजिये कि cd द्विघातीय बहुपद x2−20x+2020 के भिन्न सम्मिश्र मूलों (distinct complex roots) को दर्शाते हैं। तब
ac(a−c)+ad(a−d)+bc(b−c)+bd(b−d) का मान है
View Solutionवक्र (y−x5)2=x(1+x2)2 के बिन्दु (1,2) पर स्पर्श रेखा की प्रवणता है
View Solutionरेखा तथा वृत्त के स्पर्श बिंदु के निर्देशांक ……………. है ।
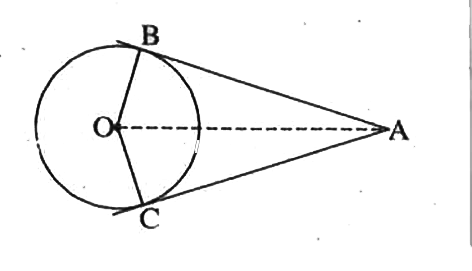
View Solutionदी गई आकृति में AB तथा AC वृत्त की स्पर्श रेखाएं है ,O वृत्त का केंद्र है ,यदि ∠CAB=60∘ तो ∠BOC है -
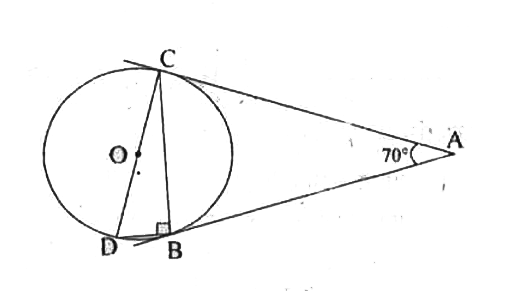
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
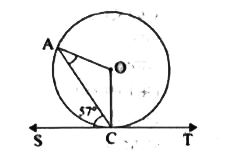
View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
View Solutionयदि किसी बिंदु P के परवलय y2=4x पर खींची गई दो स्पर्श-रेखाएँ परस्पर लम्ब हों, तो P का बिन्दुपथ है :
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solution△ABC के अन्तरगर्त वृत्त का केंद्र O है तथा भुजा AB,BC,CA क्रमशः वृत्त को बिंदु P, Q, R पर स्पर्श करती है। यदि ∠POQ=110∘,∠QOR=120∘ है ,तो ∠CAB का मान है -
View Solutionवृत्त के बाहर स्थित बिंदु से खींची गई स्पर्श रेखाओं की संख्या हो सकती है:
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solution
