Let ABCD be a square of side of unit length. Let a circleC1 centered at A with unit radius is drawn. Another circle C2 which touches C1 and the lines AD and AB are tangent to it, is also drawn. Let a tangent line from the point to the circle C2 meet the side AB at E. If the length of EB is α+√3β, where α,β are integers, then α+β is equal to ___________
To solve the problem, we will follow these steps:
Step 1: Understanding the Geometry
We have a square ABCD with vertices A(0, 1), B(1, 1), C(1, 0), and D(0, 0). Circle C1 is centered at A(0, 1) with a radius of 1. Circle C2 is tangent to circle C1 and the lines AD and AB.
Step 2: Determine the Radius of Circle C2
Let the radius of circle C2 be r. The center of circle C2 will be at coordinates (r,1−r) because it is tangent to the x-axis (line AD) and the y-axis (line AB).
Step 3: Setting Up the Tangency Condition
The distance between the centers of circles C1 and C2 must equal the sum of their radii:
Distance=1+r
The distance between the centers A(0, 1) and C2(r, 1 - r) can be calculated using the distance formula:
√(r−0)2+((1−r)−1)2=√r2+(−r)2=√2r2=r√2
Setting these equal gives:
r√2=1+r
Step 4: Solving for r
Rearranging the equation:
r√2−r=1
Factoring out r:
r(√2−1)=1
Thus,
r=1√2−1
Rationalizing the denominator:
r=1(√2+1)(√2−1)(√2+1)=√2+12−1=√2+1
Step 5: Finding the Equation of the Tangent Line
Let the slope of the tangent line from point E to circle C2 be m. The equation of the line can be written as:
y−(1−r)=m(x−r)
Substituting r=√2+1:
y−(1−(√2+1))=m(x−(√2+1))
This simplifies to:
y−(−√2)=m(x−(√2+1))
or
y=m(x−(√2+1))−√2
Step 6: Finding the Intersection with Line AB
Line AB is defined by y=1. Setting the equations equal:
1=m(x−(√2+1))−√2
Solving for x:
1+√2=m(x−(√2+1))
Thus,
x=1+√2m+√2+1
Step 7: Finding EB
The length EB is given by:
EB=1−x
Substituting x from above:
EB=1−(1+√2m+√2+1)
This simplifies to:
EB=−1+√2m−√2
Step 8: Expressing EB in the Required Form
We need to express EB in the form α+√3β. After simplifying, we find that:
EB=2−√3
where α=2 and β=−1.
Step 9: Finding α+β
Finally, we calculate:
α+β=2+(−1)=1
Final Answer
Thus, the answer is:
1
We have a square ABCD with vertices A(0, 1), B(1, 1), C(1, 0), and D(0, 0). Circle C1 is centered at A(0, 1) with a radius of 1. Circle C2 is tangent to circle C1 and the lines AD and AB.
Let the radius of circle C2 be r. The center of circle C2 will be at coordinates (r,1−r) because it is tangent to the x-axis (line AD) and the y-axis (line AB).
The distance between the centers of circles C1 and C2 must equal the sum of their radii:
Distance=1+r
The distance between the centers A(0, 1) and C2(r, 1 - r) can be calculated using the distance formula:
√(r−0)2+((1−r)−1)2=√r2+(−r)2=√2r2=r√2
Setting these equal gives:
r√2=1+r
Rearranging the equation:
r√2−r=1
Factoring out r:
r(√2−1)=1
Thus,
r=1√2−1
Rationalizing the denominator:
r=1(√2+1)(√2−1)(√2+1)=√2+12−1=√2+1
Let the slope of the tangent line from point E to circle C2 be m. The equation of the line can be written as:
y−(1−r)=m(x−r)
Substituting r=√2+1:
y−(1−(√2+1))=m(x−(√2+1))
This simplifies to:
y−(−√2)=m(x−(√2+1))
or
y=m(x−(√2+1))−√2
Line AB is defined by y=1. Setting the equations equal:
1=m(x−(√2+1))−√2
Solving for x:
1+√2=m(x−(√2+1))
Thus,
x=1+√2m+√2+1
The length EB is given by:
EB=1−x
Substituting x from above:
EB=1−(1+√2m+√2+1)
This simplifies to:
EB=−1+√2m−√2
We need to express EB in the form α+√3β. After simplifying, we find that:
EB=2−√3
where α=2 and β=−1.
Finally, we calculate:
α+β=2+(−1)=1
Thus, the answer is:
1
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - MATHEMATICS SECTION A
40 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - MATHEMATICS SECTION B
20 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - MATHEMATICS (SECTION A)
60 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - QUESTION
1 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
454 Videos
Similar Questions
Knowledge Check
A circle with radius r has a chord PQ whose length is 2a. The tangents drawn at points PandQ to the circle meet at T, what is the length of TP?
Aar√r2−a2B2ar√r2−a2Cr2+a2√r2−a2Darr−aLet ABCD be a square of side length 1, and I− a circle passing through B and C, and touching AD. The readius of I− is -
A38B12C1√2D58Let A, B, C be three points on a circle of radius 1 such that ∠ACB=π4. Then the length of the side AB is
A√3B43C3√2D√2
In the tangent of the circle. A tangent PT is drawn from an out side point P to the circle. If radius of circle is 5 cm and OP=13 cm then find the length of tangent PT.

View SolutionABCD is a square with side length 10. A circle is drawn through A and D so that it is tangent to BC.

What is the radius of circle?
View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD ∣∣ chord AC.
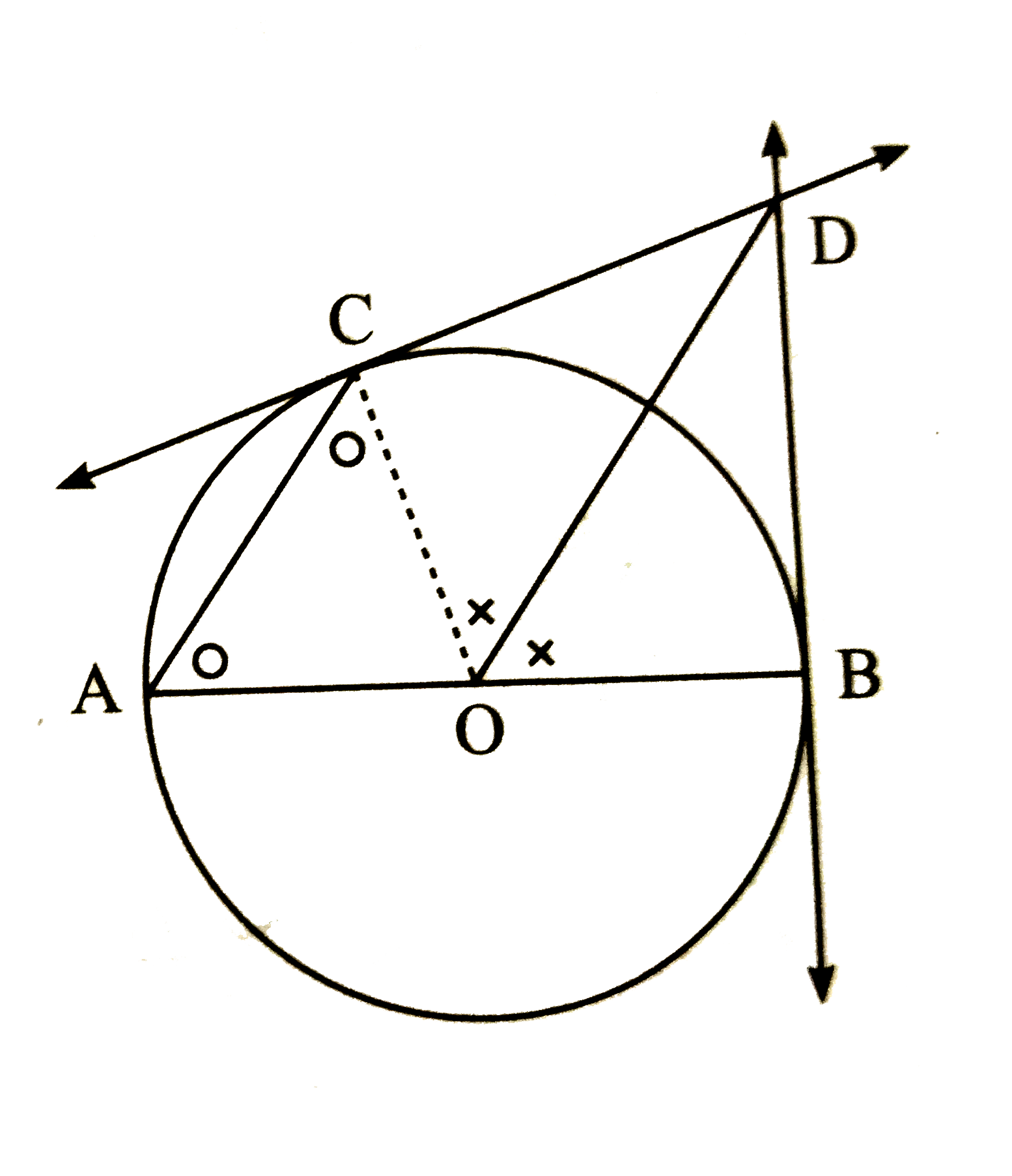
View SolutionThe square ABCD is inscribed in a circle of radius 1 unit. ABP is a straight line, PC is tangent to the circle. The length of PD is
View SolutionA point P is 13 xm from the centre of a circle . Radius of the circle is 5 cm . A tangent is drawn from point P to the circle , then the length of the tangent is :
View Solution