The image of an object placed in air formed by a convex refracting surface is at a distance of 10 m behind the surface. The image is real and is at 2rd3 of the distance of the object from the surface. The wavelength of light inside the surface is 23 times the wavelength in air. The radius of the curved surface is x13m. The value of 'x' is _________.
To solve the problem, we will follow these steps:
Step 1: Understand the Given Information
We know that:
- The image distance v=10m (behind the surface).
- The image is real and is at 23 of the object distance u.
- The wavelength of light inside the medium is 23 times the wavelength in air.
- The radius of the curved surface is x13m.
Step 2: Relate Object Distance to Image Distance
Since the image distance v is given as 10m and it is 23 of the object distance u, we can express u as:
v=23u⟹u=32v=32×10=15m
Step 3: Use the Lens Maker's Formula
For a convex lens, the lens maker's formula in terms of the refractive index μ is given by:
μ−1R=1v−1u
Where:
- μ is the refractive index of the medium.
- R is the radius of curvature.
Step 4: Calculate the Refractive Index
The refractive index μ can be calculated from the wavelength relationship:
μ=λaλm
Given that λm=23λa:
μ=λa23λa=32
Step 5: Substitute Values into the Lens Maker's Formula
Now substituting μ=32, u=15m, and v=10m into the lens maker's formula:
32−1R=110−115
Calculating the left side:
12R=110−115
Finding a common denominator for the right side:
110=330,115=230⟹110−115=330−230=130
Thus, we have:
12R=130
Step 6: Solve for R
Cross-multiplying gives:
30=2R⟹R=302=15m
Step 7: Relate R to x
We know that R=x13:
x13=15⟹x=15×13=195
Final Answer
The value of x is 195.
---
We know that:
- The image distance v=10m (behind the surface).
- The image is real and is at 23 of the object distance u.
- The wavelength of light inside the medium is 23 times the wavelength in air.
- The radius of the curved surface is x13m.
Since the image distance v is given as 10m and it is 23 of the object distance u, we can express u as:
v=23u⟹u=32v=32×10=15m
For a convex lens, the lens maker's formula in terms of the refractive index μ is given by:
μ−1R=1v−1u
Where:
- μ is the refractive index of the medium.
- R is the radius of curvature.
The refractive index μ can be calculated from the wavelength relationship:
μ=λaλm
Given that λm=23λa:
μ=λa23λa=32
Now substituting μ=32, u=15m, and v=10m into the lens maker's formula:
32−1R=110−115
Calculating the left side:
12R=110−115
Finding a common denominator for the right side:
110=330,115=230⟹110−115=330−230=130
Thus, we have:
12R=130
Cross-multiplying gives:
30=2R⟹R=302=15m
We know that R=x13:
x13=15⟹x=15×13=195
The value of x is 195.
Similar Questions
An object when placed in front of a plano-convex lens forms a real image at a distance of 10 m behind the lens. The image that is formed is one-fourth of that of the size of the object. The wavelength of light that is inside the lens is 34 times the wavelength in free space. What is the radius of the curved surface of the lens in m?
View SolutionRegion I and II are separated by a spherical surface of radius 25 cm. An object is kept in region I at a distance of 40 cm from the surface. The distance of the image from the surface is :
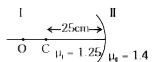
View Solution
Knowledge Check
The image of an object, forme by a plano-convex lens at a distance of 8m behind the lens, is real and is one-third the size of the object. The wavelength of light inside the lens is 23 times the wavelength is free space. The radius of the curved surface of the lens is
A1mB2mC3mD4mThe image of an object, formed by a plano-convex lens at a distance of 8 m behind the lens, is real is one-third the size of the object. The wavelength of light inside the lens is 2/3 times the wavelength in free space. The radius of the curved surface of the lens is
A1mB2mC3mD6mThe image of an object formed on the outer surface of a spoon is always
AerectBvirtualCinvertedDBoth (a) and (b)
A real image, 23 rd of the size of an object, is formed by a convex lens when the object is at a distance of 12 cm from it. Find the focal length of the lens.
View SolutionAn image is formed at a distance of 100 cm from the glass surface with refractive index 1.5, when a point object is placed in the air at a distance of 100 cm from the glass surface. The radius of curvature is of the surface is
View SolutionA point object is situated in air at a distance of 20 cm from a convex refracting surface of 5cm radius. The position of the iamge is [μ=1.5]
View SolutionAn equi-convex lens in air forms real image at distance 10cm from lens for real object. If image distance is 2/3rd of object distance. Wavelength of light in medium of lens is 2/3rd of wavelength in vacuum. Find radius of curvature of lens.
View SolutionA convex spherical refracting surfaces separates two media glass and air (μg=1.5). If the image is to be real, at what minimum distance u should the object be placed in air if R is the radius of curvature
View Solution