_________ grams of 3-Hydroxy propanal (MW=74) must be dehydrated to produce 7.8 g of acrolein (MW=56) (C3H4O) if the percentage yield is 64. (Round off to the Nearest Integer).
[Given : Atomic masses : C:12.0u, H : 1.0 u, O: 16.0 u]
To solve the problem, we need to determine how many grams of 3-Hydroxy propanal (MW = 74 g/mol) must be dehydrated to produce 7.8 g of acrolein (MW = 56 g/mol) with a percentage yield of 64%.
1. Calculate the moles of acrolein produced:
Moles of acrolein=mass of acroleinmolar mass of acrolein=7.8g56g/mol=0.1393mol
2. Determine the theoretical moles of acrolein based on the yield:
Since the percentage yield is 64%, we can express the relationship between the actual yield and theoretical yield:
Actual yield=Theoretical yield×Percentage yield
Rearranging gives:
Theoretical yield=Actual yieldPercentage yield=0.1393mol0.64=0.2170mol
3. Relate the moles of 3-Hydroxy propanal to the moles of acrolein:
The dehydration reaction of 3-Hydroxy propanal to acrolein suggests a 1:1 molar ratio. Therefore, the moles of 3-Hydroxy propanal required will also be 0.2170 mol.
4. Calculate the mass of 3-Hydroxy propanal needed:
Mass of 3-Hydroxy propanal=moles×molar mass=0.2170mol×74g/mol=16.078g
5. Round off to the nearest integer:
The mass of 3-Hydroxy propanal required is approximately 16 g.
Final Answer:
16 grams of 3-Hydroxy propanal must be dehydrated to produce 7.8 g of acrolein with a 64% yield.
---
Moles of acrolein=mass of acroleinmolar mass of acrolein=7.8g56g/mol=0.1393mol
Since the percentage yield is 64%, we can express the relationship between the actual yield and theoretical yield:
Actual yield=Theoretical yield×Percentage yield
Rearranging gives:
Theoretical yield=Actual yieldPercentage yield=0.1393mol0.64=0.2170mol
The dehydration reaction of 3-Hydroxy propanal to acrolein suggests a 1:1 molar ratio. Therefore, the moles of 3-Hydroxy propanal required will also be 0.2170 mol.
Mass of 3-Hydroxy propanal=moles×molar mass=0.2170mol×74g/mol=16.078g
The mass of 3-Hydroxy propanal required is approximately 16 g.
16 grams of 3-Hydroxy propanal must be dehydrated to produce 7.8 g of acrolein with a 64% yield.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - Chemistry (Section A)
20 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - Chemistry (Section B)
10 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - CHEMISTRY SECTION A
60 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - CHEMISTRY
150 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
561 Videos
Similar Questions
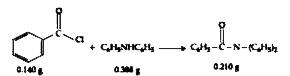
Consider the above reaction. The percentage yield of amide product is _________. (Round off to the Nearest Integer).
(Given : Atomic mass : C : 120 u, H : 10 u, N : 14.0 u, O : 16.0 u, Cl : 35.5 u)
View SolutionThe mole fraction of a solution in a 100 molal aqueous solution is _____________×10−2 ( Round off to the Nearest Integer ).
[ Given : Atomic masses : H : 1.0 u, O : 16.0 u]
View Solution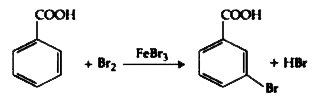
Consider the above reaction where 6.1 g of Benzoic acid is used to get 7.8 g of m-broo benzoic acid. The percentage yeild of the product is ......... (Round off to the Nearest Integer). [Give : Atomic masses : C:12.0u,H=1.0u,O=16.0,u,Br=80.0u]
View Solution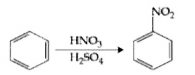
In the above reaction, 3.9 g of benzene on nitration gives 4.92 g of nitrobenzene. The percentage yield of nitrobenzene in the above reaction is _____________ %. (Round off to the Nearest Integer ).
( Given atomic mass : C : 12.0 u, H : 1.0 u, O : 16.0 u, N : 14.0 u )
View SolutionThe density of NaOH solution is 1.2gcm−3. The molality of this solution is _______ m.
(Round off to the Nearest Integer)
[Use : Atomic masses : Na : 23.0 u O : 16.0 u H : 1.0 u]
Density of H2O:1.0gcm−3]
View SolutionComplete combustion of 3 g of ethane givesx×1022 molecules of water. The value of x is _______ . (Round off to the Nearest Integer).
[Use : NA=6.023×1023 , Atomic masses in u : C : 12.0 , O : 16.0 , H : 1.0]
View SolutionWhat is the mass of 0.5 mole of wate (H2O).
(Atomic masses : H=1u,O=16u)
View SolutionA 650 molar solution of KOH (aq.) has a density of1.89gcm−3. The molarity of the solutio is ________ mol dm−3 (Round off to the Nearest Integer).
[Atomic mass :K:39.0u,O:16u,H:1.0u]
View SolutionThe pressure exerted by a non-reactive gaseous mixture of 6.4g of methane and 8.8 g of carbon dioxide in a 10L vessel at 27∘C is __________ kPa. ( Round off to the Nearest Integer ).
[ Assume gases are ideal, R = 8.314] mol−1K−1
Atomic masses : C : 120 u, H : 1.0 u, O : 16.0 u ]
View SolutionWhat is the mass of 0.5 mole of water (H2O).
(Atomic masses : H=1u,O=16u)
View Solution