जब हम एक भौतिक राशि का मापन करते है, सामान्यतः मापा गया मान यथार्थ नही होता है। इसमें कुछ त्रुटि हो सकती है जब मापे गये मान को अंकों में लिखते है, कुछ अंक विश्वसनीय तरीके से प्राप्त नही होते है तथा जिसका प्रथम अंक अविश्वसनीय होता है।
उदाहरण के लिए मानाकि पैमाने के उपयोग से कांच की पट्टिका की लम्बाई मापी जाती है। मानाकि लम्बाई 2.6 cm व 2.7 cm के मध्य स्थित है तथा हम अन्तिम रूप से लम्बाई 2.63 cm. लिख देते है। यहां अंक 2 तथा 6 विश्वसनीय है लेकिन अंक 3 अविश्वसनीय है। अब विश्वसनीय अंक तथा प्रथम अविश्वसीनय अंक सार्थक अंक कहलाता है। अतः 2.63 cm के मापन में तीन सार्थक अंक है। इन सार्थक अंको की आवश्यकता होती है। जब किसी प्रयोग में पाठ्यांक लिखा जाता है तथा इनका गणना में उपयोग किया जाता है।
नियम 1.सभी अशून्य अंक सार्थक अंक होते है। उनके मध्य दशमलव हो सकता है तथा दशमलव की स्थिति महत्वपूर्ण नही है। उदाहरण
(a) 2357 चार सार्थक अंक है।
(b) 312 तीन सार्थक अंक है।
(c) 325.23 पांच सार्थक अंक है।
(d) 23.523 पांच सार्थक अंक है।
नियम 2. दो अशून्य अंको के मध्य आने वाले सभी शून्य अंक सार्थक अंक होते है। दशमलव की स्थिति महत्वपूर्ण नहीं है। उदाहरण
(a) 2307 चार सार्थक अंक है।
(b) 320.03 पांच सार्थक अंक है । (c) 32.003 पांच सार्थक अंक है।
नियम 3. यदि संख्या बिना दशमलव के है, तब संख्या के सीमान्त अन्तिम शून्य सार्थक अंक नही है। उदाहरण
(a) 23500 तीन सार्थक अंक है।
(b) 53000 दो सार्थक अंक है।
नियम 4. दशमलव भाग में सीमान्त अन्तिम शून्य सार्थक अंक होते है। उदाहरण
(a) 3.700 चार सार्थक अंक है।
(b) 2.50 तीन सार्थक अंक है।
यहां कुछ निचित मापन दिया है जो कि पूर्ण है अर्थात्

सेवो की संख्या = 12 (ठीक exact) =12.000000............∞
इस तरह के मापन में अनन्त यर्थाथता होती है। अतः इसमें ∞ सार्थक अंक होते है।
कक्षा में विद्यार्थियों की संख्या = 125 (ठीक exact)
निर्वात में प्रकाश की चाल = 299,792,458 m/s (ठीक exact)
Mg का एक यौगिक भार से 6% Mg रखता है। यदि यौगिक का न्यूनतम मोलर द्रव्यमान n×10z g/mol है। कैफीन का अणुभार 194 है। इसमें भार के अनुसार लगभग 30% नाइट्रोजन है। इसके एक अणु में नाइट्रोजन के परमाणुओं की संख्या m है। m/n का मान दीजिए।
The correct Answer is:1
माना की योगिक का मोलर द्रव्यमान M है abhikriya k
(इसलिए) M×6100=24
m= 400 g/mole
Topper's Solved these Questions
Similar Questions
निम्न में से कौनसे नमूने 3NA परमाणु रखते हैं :
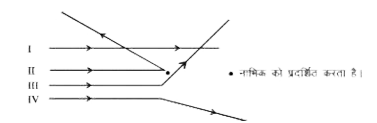
View Solutionα− कण प्रकीर्णन प्रयोग में α− कण का कौनसा/कौनसे पथ सम्भव है ?
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionअंकों 1,2,3,4 से 4 अंकों की संख्या बनाई जाती है जिसमें अंकों की पुनरावृत्ति नहीं हो सकती है, तब संख्या के विषम होने की प्रायिकता है
View Solutionयदि 4964A, 9 से विभाज्य है तो अंक A का मान क्या हो सकता है?
View Solutionयदि संख्या 354Y2, 6 का एक गुणज है तो Yअंक का मान क्या हो सकता है?
View Solutionकिसी परीक्षा में एक छात्र को 40% अंक प्राप्त होते हैं तथा वह 20 अंकों से असफल हो जाता है। उसी परीक्षा में दूसरे ,छात्र को 45% 'अंक प्राप्त होते हैं, तथा उसके प्राप्त अंक पास होने के लिए न्यूनतम अंक से 5 अधिक है। परीक्षा का पूर्णांक ज्ञात कीजिए।
View Solutionसही कथनों का चयन कीजिए।
(1) जब क्लोरीन गैस को फेरस ब्रोमाइड के विलयन के माध्यम से बुदबुदाया जाता है तो फेरिक ब्रोमाइड प्राप्त होता है।
(2) जब SO2(g),H2O(g) और वायु को गर्म सोडियम क्लोरीन पर प्रवाहित किया जाता है तो सोडियम सल्फेट प्राप्त होता है।
(3) जब एलुमिनियम सल्फाइड आर्द्र हो जाता है। तब H2S गैस मुक्त होती है।
View Solutionजब एल्कोहॉल की वाष्प को गर्म तांबे के ऊपर से गुजारा जाता है, तो एल्कोहॉल शीघ्रता से एल्कीन में रूपांतरित हो जाती है, एल्कोहॉल है:
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionजब AgNO_(3) के विलयन को आधिक्य में CoCl_(3).XNH_(3) विलयन के 1M में मिलाया जाता है, तो AgCI के एक मोल का निर्माण होता है? 'X' का मान क्या है? (माना लीजिए कि उपसहसंयोजन संख्या 6 है।)
View Solutionजब गैस को जल के माध्यम से 298K पर बुदबुदाया जाता है, तब गैस का एक तनु विलयन प्राप्त होता है। गैस के लिए हेनरी स्थिरांक 100 Kbar है। यदि गैस 1 बार का दाब डालती है, तो 1 लीटर जल में विलीन गैस के मोलो की संख्या x×10−5 है। यहाँ x का मान ज्ञात कीजिए?
View Solutionजब logk और 1/T के बीच एक आलेख आलेखित किया जाता है, तो हमें एक आलेख प्राप्त होता है, जैसा कि नीचे दर्शाया गया है आलेख में ढाल का मान क्या है?
View Solutionऐडिनिन न्यूक्लिक अम्ल के न्यूक्लियोटाइडों के निर्माण में शामिल दो प्यूरीन क्षारों में से एक है। ऐडिनिन का अणुसूत्र CxHxNx होता है, तो 'x' का मान है
View Solutionएक अभिक्रिया A में प्रथम कोटि तथा B में द्वितीय कोटि है: जब A और B दोनों की सांद्रता दोगुनी हो जाती है, तो दर कैसे प्रभावित होती है?
View Solutionजब कॉपर नाइट्रेट को प्रबलता से गर्म किया जाता है, तो कौनसा यौगिक प्राप्त होता है?
View Solution
