m द्रव्यमान के तीन कण स्थिर घर्षणरहित क्षैतिज वृत्ताकार पथ पर समान क्षैतिज तल में चित्रानुसार फिसल सकते है। प्रत्यावस्थान गुणांक e= 0.5 है। यह मानिये कि m2 तथा m3 प्रारम्भ में विराम पर है तथा टक्कर के पहले त्रिज्यीय रेखा के अनुदिश स्थित है, तथा स्प्रिंग प्रारम्भ में मूल लम्बाई में है। तब अगली गति में स्प्रिंग में अधिकतम् विस्तार होगा।

34V0√mk
34V0√m5k
34V0√2m5k
35V0√mk
The correct Answer is:B
टक्कर के ठीक पश्चात् वेग
V0=V1+V2 ...............(A)
12=−V1+V2V0
−V1+V2=V02...........(B)
A तथा B से
⇒V1=V04 & V2=3V04
जब अधिकतम् विस्तार होगा तब द्रव्यमान m, तथा mg के केन्द्र के सापेक्ष कोणीय चाल समान होगी। वृत्त के केन्द्र के सापेक्ष कोणीय संवेग संरक्षण से

m34V0(2R)+0=mR2ω+m(2R)2ω
ω=310V0R
अतः m2 का वेग =35V0
तथा m3 का वेग =310V0
जब विस्तार अधिकतम् हो तब ऊर्जा संरक्षण के उपयोग से
12m(34V0)2=12m(35V0)2+12m(310V0)2+12kx2max⇒xmax=34V0√m5k
Topper's Solved these Questions
Similar Questions
कोई अर्धगोला एकसमान धनावेशित है। गोले के केन्द्र से परे इसके किसी व्यास पर (अर्द्ध गोले की सीमा के भीतर) स्थित बिन्दु पर जो केन्द्र से दूर है, विद्युत क्षेत्र की दिशा
View Solutionनिम्न में से असत्य कथन है
[a] एक वस्तु की अचर चाल तथा परिवर्ती त्वरण हो सकता है।
[b] एक वस्तु का किसी क्षण पर वेग शून्य एवं अशून्य त्वरण हो सकता है।
[c] एक वस्तु का अचर वेग तथा एक समान त्वरण हो सकता है।
View Solutionकुछ रसायनों के संपर्क में अधिक समय तक रहने पर, शरीर में पैदा ………………… हो सकती है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionएक वस्तु जिसका द्रव्यमान m है विराम से h ऊँचाई से गुरुत्वीय त्वरण g के अन्तर्गत गिरती है तथा यह रेत में गहराई d तक धंसती है। रेत में फँसने के दौरान औसत मन्दन होगा
View Solution(1+x)2n के प्रसार में महत्तम गुणांक है
View SolutionS_(N) अभिक्रियाओं में RCOOH तथा RCOCI में से किसकी क्रियाशीलता अधिक है तथा क्यों ?
View Solutionयदि कोई बिंदु P,yz तल में स्थित है तो yz तल में उस बिंदु के निर्देशांक ___________के रूप में होंगे
View Solutionवर्तिकाग्र स्त्रीकेसर के ...... में स्थिर होता है।
View Solution"बेटी की आँखें मंदिर में दीवट पर जलते घी के दो दिए है" में कौन-सा अलंकार है?
View Solutionप्राथमिक स्तर पर बच्चों के शुरुआती भाषा-विकास में सर्वाधिक योगदान दे सकते/सकती है/है
View Solutionयदि P, Q के उत्तर दिशा में तथा R,P के दक्षिण-पश्चिम में तथा S, Q के उत्तर-पूर्व में है, तो इनमे से कौन-सा निश्चित रूप से सत्य है?
View Solutionनिम्नलिखित में से कौन-सा, कनाडा, चिली तथा जर्मनी के समान है?
View Solutionअभिक्रिया अनुक्रम में,
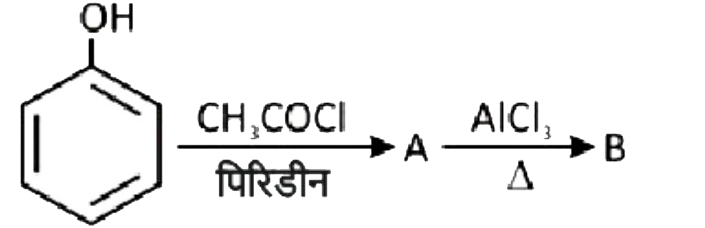
B के संबंध में सही कथन है:
View Solutionनिम्नलिखित संकुलों के युग्म में से किस स्थिति में केंद्रीय परमाणुओं में संकरण तथा प्रभावी परमाणु क्रमांक के मान समान है?
View Solution
