एक गतिशील कण पर बहुत सारे बल F1,F2,F3,….. कार्यरत है। इनमे से एक बल को लेते हैं। माना यह F2 है, तो निम्न में से कौनसा तथ्य F2 के बारे में सत्य होगा -
F2 के द्वारा किया गया कार्य ऋणत्मक होगा यदि कण की चाल कम हो रही है।
F2 के द्वारा किया गया कार्य धनात्मक होगा यदि कण की चाल बढ़ हो रही है।
F2 के द्वारा किया गया कार्य अन्य बलों द्वारा किये गए कुल कार्य के तुल्य होगा यदि कण की चाल नहीं बदलती है।
यदि F2 संरक्षी बल हो, तो सभी अन्य बलों द्वारा किया गया कार्य, बल F2 के कारण स्थितिज ऊर्जा में परिवर्तन के तुल्य होगा जब चाल नियत है।
The correct Answer is:D
Step by step video, text & image solution for एक गतिशील कण पर बहुत सारे बल F_(1), F_(2), F_(3),….. कार्यरत है। इनमे से एक बल को लेते हैं। माना यह F_(2) है, तो निम्न में से कौनसा तथ्य F_(2) के बारे में सत्य होगा - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
तीन वृत्ताकार चाप, प्रत्येक की त्रिज्या R एवं उन पर कुल आवेश चित्र में दर्शाये गये है। वक्रता केन्द्र पर परिणामी वैधुत विभव है -
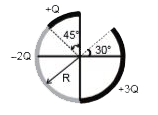
View Solution
View SolutionLet f1:R→Randf2:C→C are two functions such that f1(x)=x3andf2=x3.Prove that f1andf2are not same.
View SolutionIf F1andF2 aare two vectors of equal magniudes F such that |F1.F2|=|F1×F2|,then|F1+F2| equals to
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View SolutionIf f1(x)=2x+3,f2(x)=3x2+5,f3(x)=x+cosx are defined from R→R, then f1,f2 and f3 are
View SolutionGiven F1=1,F2=3andFn=Fn−1+Fn−2 then F5 is
View SolutionGiven F1=1,F2=3andFn=Fn−1+Fn−2 then F3 is ____.
View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
View Solutionनिम्न कथन पर विचार कीजिये ''P(n)=n2−n+41 एक अभाज्य संख्या है'' तो इनमे से कौन-सा एक सत्य है?
View Solutionयदि z एक सम्मिश्र संख्या है, तो निम्न में से कौन-सा कथन सत्य है?
View Solutionएक कण पर लगे समान परिमाण वाले तीन बल संतुलन में हैं, तो उनके बीच व कोण _____ होगा।
View Solutionf1(x)=x+a,f2(x)=x2+bx+c and Δ=∣∣ ∣ ∣∣111f1(x1)f1(x2)f1(x3)f2(x1)f2(x2)f2(x3)∣∣ ∣ ∣∣, then Δ is independent of
View Solutionदो सदिशों F1 व F2 का परिमाण समान है जिसका मान F है। यदि |F1⋅F2|=|F1×F2| तब |F1+F2| बराबर है
View SolutionIf F_(1) and F_(2) are two vectors of equal magnitudes F such that |F_(1).F_(2)|= |F_(1)xxF_(2)|, "then"|F_(1) +F_(2)| equals to
View SolutionIf f1(x)=2x+3,f2(x)=3x2+5,f3(x)=x+cosx are defined from R→R, then f1,f2 and f3 are
View Solution
