जोड़े -
x2+y2,2x2−y2+5 एवं −x2+2y2−4
The correct Answer is:2x2+2y2+1
Step by step video, text & image solution for जोड़े - x^(2)+y^(2),2x^(2)-y^(2)+5 एवं -x^(2)+2y^(2)-4 by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- बीजीय व्यंजक BOOK - STUDENTS FRIENDSCHAPTER - बीजीय व्यंजक EXERCISE - Exercise 5C
30 Videos
- बीजीय व्यंजक BOOK - STUDENTS FRIENDSCHAPTER - बीजीय व्यंजक EXERCISE - Exercise 5D
3 Videos
- बीजीय व्यंजक BOOK - STUDENTS FRIENDSCHAPTER - बीजीय व्यंजक EXERCISE - Exercise 5A
40 Videos
- प्रायोगिक ज्यामिति (ज्यामितीय रचना)BOOK - STUDENTS FRIENDSCHAPTER - प्रायोगिक ज्यामिति (ज्यामितीय रचना)EXERCISE - Exercise 11 B
38 Videos
- भिन्न एवं दशमलव BOOK - STUDENTS FRIENDSCHAPTER - भिन्न एवं दशमलव EXERCISE - EXERCISE 2F (Type III. एक दशमलव संख्या में दूसरे दशमलव संख्या से भाग देने पर आधारित प्रश्न : )
13 Videos
Similar Questions
यदि a=−2 तो a2+a+1 का मान ज्ञात करें।
View Solutionबराबर लम्बाई के रेखाखंडो से बनाए गए अंको के निम्नांकित पैटर्न को देंखे तथा n=5,10,100 के लिए रेखाखंडो की संख्या बताएँ।
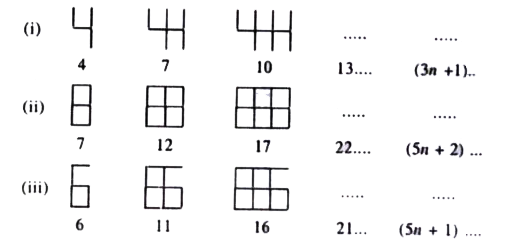
View Solutionनिम्नलिखित स्थितियों में, चरों, अचरों और अंक गणितीय संक्रियाओं का प्रयोग करते हुए, बीजीय व्यंजक प्राप्त कीजिए :
संख्या x को स्वयं उससे गुणा किया जाता है।
View Solutionएक त्रिभुज ABC बनाये जिसमें AB = 6 सेमी, BC = 7 सेमी तथा CA = 5.5 सेमी।
View Solutionज्ञात करें:
36÷0.2
View SolutionThe equation of the transvers and conjugate axes of a hyperbola are, respectively, x+2y−3=0 and 2x−y+4=0 , and their respective lengths are √2 and 2√3. The equation of the hyperbola is
a) 25(x+2y−3)2−35(2x−y+4)2=1
b) 25(x−y−4)2−35(x+2y−3)2=1
c)2(2x−y+4)2−3(x+2y−3)2=1
d)2(x+2y−3)2−3(2x−y+4)2=1
View SolutionThe equation of the normal to the curve y=x(2−x) at the point (2, 0) is x−2y=2 (b) x−2y+2=0 (c) 2x+y=4 (d) 2x+y−4=0
View SolutionSimplify: 5+[x−{2y−(6x+y−4)+2x2}−(x2−2y)]
View SolutionThe angle of intersection of the circles x2+y2=4 and x2+y2+2x+2y, is
View Solutionनिम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए -
(x+2y)2+5(x+2y)(2x+y)+6(2x+y)2
View SolutionIf x^2+y^2=7 and xy=2 then x^4-2x^2y^2+y^4=
View SolutionThe equation of the transvers and conjugate axes of a hyperbola are, respectively, x+2y−3=0 and 2x−y+4=0 , and their respective lengths are √2 and 2√3. The equation of the hyperbola is
a) 25(x+2y−3)2−35(2x−y+4)2=1
b) 25(x−y−4)2−35(x+2y−3)2=1
c)25(2x−y+4)2−35(x+2y−3)2=1
d)2(x+2y−3)2−3(2x−y+4)2=1
View SolutionThe equation of the normal to the curve y=x(2−x) at the point (2, 0) is
(a)x−2y=2
(b) x−2y+2=0
(c) 2x+y=4
(d) 2x+y−4=0
View SolutionSimplify: 5+[x−{2y−(6x+y−4)+2x2}−(x2−2y)]
View SolutionMultiply: (i) (2x2y2−5xy2)by (x2−y2) (ii)(x7+x22)by (25+9x4)
View Solution
