If r =7 cm and θ = 36∘, then area of sector is……Solution in Marathi
(A) 15.4 cm2
(B) 20.36 cm2
( C) 10.46 CM2
(D) 18.2 cm2
Step by step video & image solution for If r =7 cm and theta = 36^@, then area of sector is…… by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
To draw graph of 4x+5y=19,find y when x=1. Options: a) 4 b) 3 c) 2 d) -3
View SolutionWhat is the ratio of 1mm to 1cm?
View SolutionThe area of a sector of angle θ∘ of a circle with radius R is
View Solutionएक 36 सेमी त्रिज्या वाले वृत्त के एक त्रिज्यखण्ड का क्षेत्रफल 54π वर्ग सेमी है। इस त्रिज्यखण्ड के संगत चाप की लम्बाई ज्ञात कीजिए।
View SolutionIf the length of an arc of sector of a circle is 20 cm and if its radius is 7 cm, find the area of the sector.
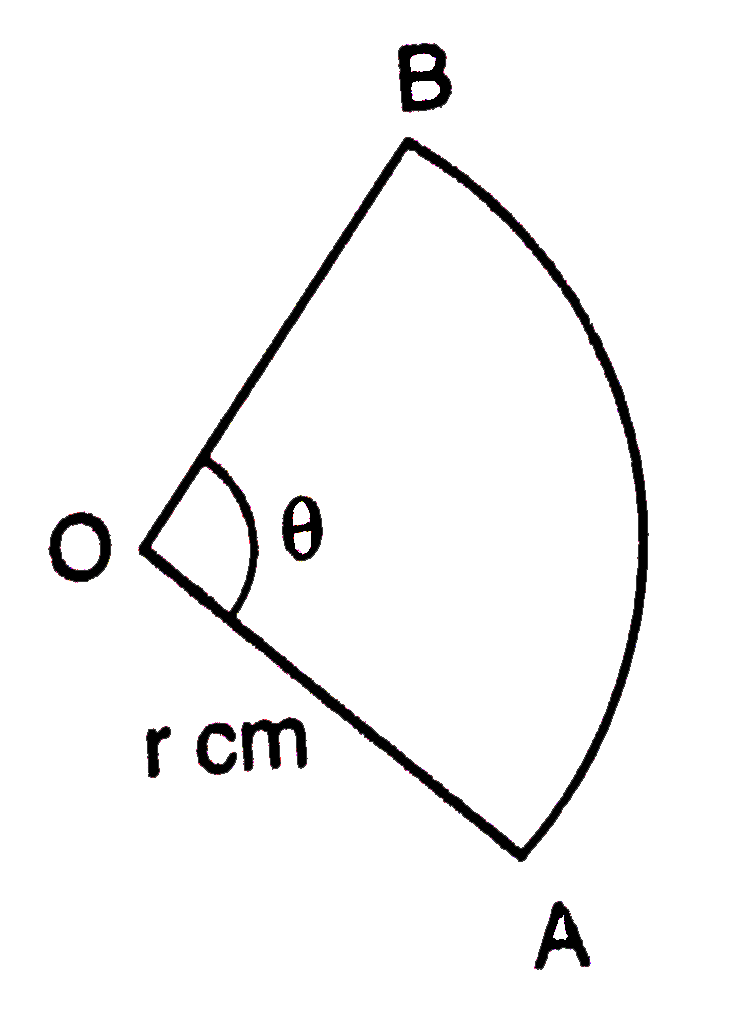
View Solutionचित्र में एक वृत्त का त्रिज्यखण्ड जिसकी त्रिज्या r सेमी. तथा कोण θ∘ है | त्रिज्यखण्ड का क्षेत्रफल A वर्ग सेमी. तथा इसका परिमाप 50 सेमी. हो, तो सिद्ध कीजिए कि :

θ=360π(25r−1)
View Solutionचित्र में एक वृत्त का त्रिज्यखण्ड जिसकी त्रिज्या r सेमी. तथा कोण θ∘ है | त्रिज्यखण्ड का क्षेत्रफल A वर्ग सेमी. तथा इसका परिमाप 50 सेमी. हो, तो सिद्ध कीजिए कि :
A=25r−r2
View SolutionRadius of a sector of a circle is 7 cm. If measure of arc of the sector is 210∘ Find the area of sector
View SolutionIf θ is the angle (in degrees) of a sector of a circle of radius r, then area of sector is
View Solutionr त्रिज्या के वृत्त के एक त्रिज्यखंड का केंद्रीय कोण θ (डिग्री में ) है, तो त्रिज्यखंड का क्षेत्रफल होगा -
View Solutionx∘=60∘,r=14 cm then area of sector = ………. cm2
View SolutionThe area of a sector of a circle of radius 36 cm is 72tccm2.The length ofthe corresponding arc of the sector is
View SolutionFigure shows a sector of a circle of radius r containing an angle θ∘ The area of the sector is Acm2 and the perimeter is 50cm. Prove that θ=360π(25r−1) and A=25r−r2
View SolutionRadius of a sector of a circle is 7 cm. If measure of arc of the sector is 30∘find the area of the sector
View SolutionIf θ is the angle (in degrees) of a sector of a circle of radius r, then area of sector is
View Solution
