सम्मिश्र संख्याओं z में जो प्रतिबन्ध ।z+1−i।≤1 को संतुष्ट करती है , न्यूनतम धनात्मक कोणाक वाली संख्या है
1−i
−1+i
−i
इनमे से कोई नहीं
The correct Answer is:D
Step by step video, text & image solution for सम्मिश्र संख्याओं z में जो प्रतिबन्ध । z +1 -i। le 1 को संतुष्ट करती है , न्यूनतम धनात्मक कोणाक वाली संख्या है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT HINDICHAPTER - सम्मिश्र संख्याएँEXERCISE - प्रश्नावली (विगत वर्षों के प्रश्न )12videos
सम्मिश्र संख्याएँ
- BOOK - ARIHANT HINDICHAPTER - सम्मिश्र संख्याएँEXERCISE - प्रश्नावली स्तर 2 विगत वर्षो के प्रश्न18videos
सम्मिश्र संख्याएँ
- BOOK - ARIHANT HINDICHAPTER - सम्बन्ध तथा फलन EXERCISE - प्रारम्भिक प्रश्नावली 37videos
सम्बन्ध तथा फलन
- BOOK - ARIHANT HINDICHAPTER - सरल रेखाEXERCISE - प्रश्नावली स्तर-2 (विगत वर्षों के प्रश्न)12videos
सरल रेखा
Similar Questions
यदि z≠1 तथा z2z−1 वास्तविक है, तो z द्वारा निरूपित सम्मिश्र संख्या वाला बिन्दु
03:36View Solutionयदि सम्मिश्र संख्या z का मापांक इकाई तथा कोणान्क θ है, तब arg(1+z1+¯z) बराबर होगा
06:13View Solutionनिम्न में से कौन-सा सम फलन है?
03:59View Solutionरेखा x + y= | a | तथा ax - y = 1 प्रथम चतुर्थांश में प्रतिच्छेद करते हैं, तब 'a' के सभी सम्भव मान निम्न अन्तराल में हैं
03:36View Solutionसम्मिश्र संख्या z=x+y का बिन्दुपथ कीजिए, यदि
(a)|z|=a (b)|z−i|=2 (c)|z+1−2i|=√7.04:59View Solutionयदि ज्यामिति आरेख पर बिन्दु P सम्मिश्र संख्या z=x+iy को निरूपित करता है , तो P का बिन्दुपथ ज्ञात कीजिए जबकि
(a)|z−1|=|z−3| (b)|z−1|=5|z+1| (c)arg(z−3)=π303:07View Solutionसम्मिश्र संख्याओं z कि संख्या जो इस प्रकार |z−1|=|z+1|=|z−i|है, है :
04:11View Solutionयदि आरगंड आरेख पर बिन्दु P सम्मिश्र संख्या z = x + iy को निरूपित करता है, तो P का बिन्दुपथ ज्ञात कीजिए जबकि ∣∣∣z−2z+2∣∣∣=5
05:31View Solutionसिध्द कीजिए कि बिन्दु z का बिन्दुपथ जो प्रतिबन्ध argz−1z+1=π3 को संतुष्ट करता है, होगा - x2+y2−2√3y−1=0
08:08View Solutionसम्मिश्र संख्या 1 + i का कोणांक …………. है ।
07:26View Solutionदिये गये चित्र में छायांकित भाग निम्न सुसंगत क्षेत्र को दर्शाता है -
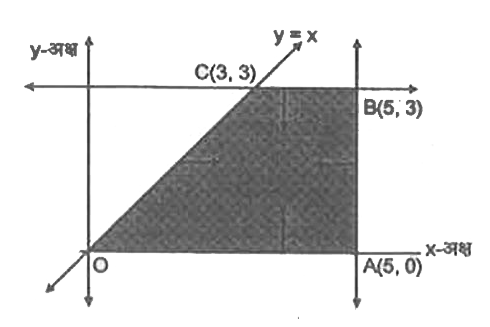
तो प्रतिबन्ध है -06:12View Solutionयदि z=x+iy और w=(1−iz)(z−i), तब |w|=1 सम्मिश्र तल में इंगित करता है कि
04:45View Solutionमाना z1=10+6i और z2=4+6i यदि सम्मिश्र संख्या z इस प्रकार है कि (z−z1)(z−z2) का कोणांक π4 है, तो सिद्ध कीजिए कि |z−7−9i|=3√2.
03:28View Solutionमाना कि ω=cos2π3+i sin 2π3 एक सम्मिश्र संख्या है, तो ∣∣ ∣ ∣∣z+1ωω2ωz+ω21ω21z+ω∣∣ ∣ ∣∣=0 को संतुष्ट करने वाली विभिन्न सम्मिश्र संख्याओं z की संख्या है।
04:41View Solutionमाना ω एक सम्मिश्र संख्या ऐसी है कि 2ω+1=z जहाँ, z=√−3 है। यदि ∣∣ ∣ ∣∣1111−ω2−1ω21ω2ω2∣∣ ∣ ∣∣=3k है तो k बराबर है
02:23View Solutionमाना z∈C जिसके लिए Im (z) = 10 तथा किसी प्राकृत संख्या n के लिए यह 2z−n2z+n=2i−1 को संतुष्ट करता है , तो
03:19View Solution

