A point P(x,y) is such that its distance from the fixed point is equal to its distance from y-axis. Prove that the equation of the locus is given by, .Solution in Odia
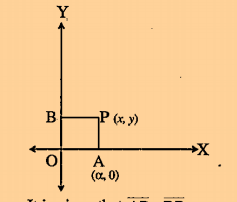
It is given that
or,
or,
or,
which is the locus of the point P(x,y).
Topper's Solved these Questions
Similar Questions
If the values observed are 1,2,…..,n each with frequency 1, find the mean value
View SolutionThe number of lines making equal angles with coordinate axes is_____.
View SolutionP is a point,whose distance from point (2,0) and perpendicular distance from line 2x+alpha y4=0(a in R) are equal,the locus of P is
View SolutionDistance of any point P(x,y) from origin is defined by d=max{|x|,|y|} and if alpha^(2)+beta^(2)-2 alpha+4 beta+5=0, then distance of A(alpha,beta) from origin is .....
View SolutionA point P(x,y) moves in the xy - plane in such a way that its distance from the point (0,4) is equal to 23 rd of its distance from the x axis , find the equation to the locus of P.
View SolutionThe equation of the locus of the point whose distance from x - axis is twice its distance from the y - axis, is
View Solutionयदि एक बिंदु इस प्रकार चले कि उसकी बिंदु (a,0) तथा y-अक्ष से दूरी बराबर हो , तो उसके बिन्दुपथ का समीकरण है :
View SolutionIf a point P moves such that its distances from the point A(1,1) and the line x+y+2=0 are equal, then the locus of P is
View Solutionउस बिन्दु का बिन्दुपथ जो इस प्रकार गति करता है कि उसकी बिन्दु (0, 0) से दूरी, उसकी Y-अक्ष से दूरी की दोगुनी है, हैं
View SolutionFind the equation to the locus of a point P whose distance to (2,0)is equal to its distance from y-axis.
View SolutionFind the equation to the locus of a point P whose distance to (2,0) is equal to its distance from y-axis.
View SolutionThe equation of the locus of the point whose distance from x-axis is twice its distance from the y-axis is
View SolutionThe distance of the point P(α,β,γ) from y-axis is
View SolutionFind the locus of the point such that its distance from the y-axis is equal to its distance from the point (1, 1).
View SolutionFind the equation of the locus of a point whose distance from the y-axis is equal to its distance from (2,1,−1).
View Solution
