नीचे दिखाये गये निकाय में दो समान द्रव्यमान m तथा स्प्रिंग-नियतांक K की एक स्प्रिंग है। बांये द्रव्यमान तथा क्षतिज मेज के बीच घर्षण गुणांक μ है, तथा घिरनी घर्षणरहित है। दोनो ब्लॉकों से जुड़ी डोरी द्रव्यमानहीन तथा अविता न्य है। निकाय की स्प्रिंग को प्राकृतिक लम्बाई (बिना खिंची लम्बाई) की अवस्था में रखा जाता है तथा फिर निकाय को छोड़ दिया जाता है।
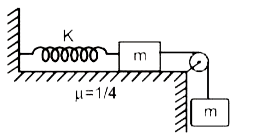
स्प्रिंग का विस्तार (extension), जब द्रव्यमान पहली बार क्षणिक विरामावस्था में आते हैं, होगा (μ=1/4)
3mg2K
mg2K
mgK
2mgK
The correct Answer is:A
कार्य-ऊर्जा प्रमेय से, द्रव्यमान रूक जाते है जब उन पर किया गया कुल कार्य शून्य होता हैI
W=mgx−12kx2−μmgx=0
∴2mgk(1−μ)=3mg2k
Topper's Solved these Questions
Similar Questions
यदि →A=ˆi+2ˆj+3ˆk & →B=3ˆi−2ˆj+ˆk, हो तो →A तथा →B से बनने वाले समांतर चतुर्भुज का क्षेत्रफल होगा जहाँ उपरोक्त दोनों सदिश इसकी भुजाएं हैं :
View Solutionवत्ताकार पथ में चलने वाले कण के रेखिक वेग, उसके स्थिति सदि । व कोणीय वेग में सम्बन्ध होता है|
View Solutionकिसी निकाय में दो आवेश qA=2.5×10−7C तथा qB=−2.5×10−7C क्रमश: दो बिंदुओं A:(0,0,−15cm) तथा B:(0,0,+15) पर स्थित है। निकाय का कुल आवेश तथा विद्युत द्विध्रुव आघूर्ण क्या है?
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionघिरनी निकाय |स्प्रिंग बल
View Solutionस्प्रिंग द्रव्यमान निकाय
View Solutionस्प्रिंग (कमानी) द्रव्यमान निकाय की सरल आवर्त गति
View Solutionस्प्रिंग द्रव्यमान निकाय पर कुछ महत्वूर्ण प्रश्न
View Solutionस्प्रिंग ब्लॉक निकाय के दोलन
View Solutionरेसिमिक मिश्रणों के d तथा । प्रतिबिंब समावयवियों में पृथक्करण की प्रक्रिया को कहा जाता है :
View SolutionRevision|स्प्रिंग स्थितिज ऊर्जा तथा स्प्रिंग - ब्लॉक निकाय (स्प्रिंग बल द्वारा किया गया कार्य)|स्प्रिंग बल से संबंधित स्थितिज ऊर्जा|Case|Quiz|OMR|Summary
View SolutionRevision|स्प्रिंग स्थितिज ऊर्जा तथा स्प्रिंग- ब्लॉक निकाय|OMR|Summary
View Solution
