यदि a, b, c तीन विभिन्न वास्तविक संख्याऐं इस प्रकार है ताकि Q,(x)=ax2+bx+c,Q2(x)=bx2+cx+a और Q3(x)=cx2+ax+b सदैव अऋणात्मक है, तब व्यंजक y=a2+b2+c2ab+bc+ca के परिसर से संभावित पूर्णांक है -
1
2
3
4
The correct Answer is:B, C, D
Topper's Solved these Questions
Similar Questions
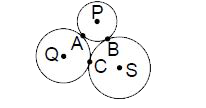
P,Q एवं S केन्द्र वाले वृत्त चित्रानुसार परस्पर बिन्दु A, B एवं C पर बाह्यतः स्पर्श करते हैं। यदि P,Q एवं S केन्द्र वाले वृत्तों की त्रिज्याएँ क्रमशः 1,2 व 3 है, तो जीवा AB की लम्बाई ____________ है
View Solutionयदि f(x)=4x2−4ax+a2−2a+2, X के पदों में कोई द्विघात बहुपद एवं 'a ' कोई वास्तविक संख्या है |
यदि परवलय y=f(x) के शीर्ष का x निर्देशांक 0 से छोटा तथा f(x) का अन्तराल X∈[0,2] मे न्यूनतम मान 3 हो, तो a का मान है-
View Solutionlimx→1ax2+bx+ccx2+bx+a,a+b+c≠0
View Solutionif x^(2)+x+1 is a factor of ax^(3)+bx^(2)+cx+d then the real root of ax^(3)+bx^(2)+cx+d=0 is : (a) -(d)/(a)(B)(d)/(a) (C) (a)/(b) (D)none of these
View SolutionLet a, b, c be three distinct real numbers such that each of the expressions ax^+bx +c, bx^2 + cx + a and ax^2 + bx + c are positive for all x in R and let alpha=(bc +ca+ab)/(a^2+b^2+c^2) then (A)alpha 1/4 (D) alpha>1
View SolutionSimply 1x+a+1x+b+1x+c+axx3+ax2+bxx3+bx2+cxx3+cx2
View SolutionIf a,b,c are distinct positive real numbers such that the quadratic expression Q1(x)=ax2+bx+c, Q2(x)=bx2+cx+a,Q3(x)=cx2+x+b are always non-negative, then possible integer in the range of the expression y=a2+b2+c2ab+bc+ca is
View Solutionमाना a,b,c वास्तविक संख्याएं है। माना x,y,z ऐसी वास्तविक संख्या है जो कभी शून्य नहीं हैं तथा x=cy+bz,y=az+cx तथा z=bx+ay, तो a2+b2+c2+2abc का मान है:
View Solutionयदि f(x)=x3+bx2+cx+d और 0<b2<c, तब (−∞,∞) में
View Solutionयदि समीकरण x2−bxax−c=λ−1λ+1 के मूल α व β इस प्रकार है कि α+β=0 तब λ का मान है
View Solutionयदि α,β समीकरणax2+bx+c=0 के मूल हों , तबlimx→α1−cos(ax2+bx+c)(x−α)2 का मान है
View Solution1x+a+1x+b+1x+c+axx3+ax2+bxx3+bx2+cxx3+cx2 को सरल कीजिए।
View SolutionEvaluate limx→1ax2+bx+ccx2+bx+a,a+b+c≠0
View Solutionif x^2+x+1 is a factor of ax^3+bx^2+cx+d then the real root of ax^3+bx^2+cx+d=0 is : (a) -d/a (B) d/a (C) a/b (D)none of these
View SolutionShow that ∣∣ ∣ ∣∣a2+x2ab−cxac+bxab+cxb2+x2bc−axac−bxbc+axc2+x2∣∣ ∣ ∣∣=∣∣ ∣∣xc−b−cxab−ax∣∣ ∣∣2.
View Solution
