निम्नलिखित में सत्य और असत्य बताइए
(a) व्यास पर सिर्फ एक त्रिज्या चिन्हित किया जा सकता है
(b) वृत की त्रिज्या सदैव व्यास से आधी नहीं होती है
(c ) वृत में अपरिमित संख्या में त्रिज्याएँ होती है
(d) व्यास वृत की परिसीमा बनाती है
(e ) किसी वृत के वृतीय क्षेत्र में वृत का अभ्यंतर एवं स्वयं वृत सम्मिलित रहता है
The correct Answer is:(a) असत्य (b) असत्य (c ) सत्य (d) असत्य (e ) सत्य
Step by step video, text & image solution for निम्नलिखित में सत्य और असत्य बताइए (a) व्यास पर सिर्फ एक त्रिज्या चिन्हित किया जा सकता है (b) वृत की त्रिज्या सदैव व्यास से आधी नहीं होती है (c ) वृत में अपरिमित संख्या में त्रिज्याएँ होती है (d) व्यास वृत की परिसीमा बनाती है (e ) किसी वृत के वृतीय क्षेत्र में वृत का अभ्यंतर एवं स्वयं वृत सम्मिलित रहता है by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023Topper's Solved these Questions
- आधारभूत ज्यामितीय अवधारणाएँBOOK - STUDENTS FRIENDSCHAPTER - आधारभूत ज्यामितीय अवधारणाएँEXERCISE - अभ्यास 4(E )
5 Videos
- आँकड़ों का प्रयोग BOOK - STUDENTS FRIENDSCHAPTER - आँकड़ों का प्रयोग EXERCISE - EXERCISE 9( C )
5 Videos
- ऋणात्मक संख्याएँ और पूर्णांक BOOK - STUDENTS FRIENDSCHAPTER - ऋणात्मक संख्याएँ और पूर्णांक EXERCISE - Exercise 6(B)
33 Videos
Similar Questions
निम्नकिंत आकृतियों में चतुर्भुज की पहचान करे
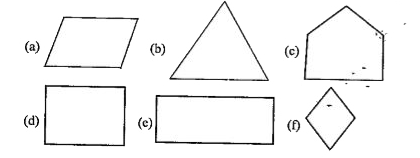

View Solutionएक स्कूल के 120 छात्रों का इस आशय से सर्वेक्षण किया गया कि वे अपने खाली समय में किस क्रियाकलाप को पसंद करते हैं। निम्नांकित आँकड़ें प्राप्त हुए।

1 इकाई लम्बाई = 5 छात्र का पैमाना लेकर एक दण्ड आलेख बनाइये। खेलने के अतिरिक्त कौन - सा क्रियाकलाप अधिकांश छात्रों द्वारा पसंद किया गया है।
View Solutionघटायें : −15−(18)
View Solutionवृत के क्षेत्रफल में परिवर्तन कि दर इसकी त्रिज्या r के सापेक्ष ज्ञात कीजिए जबकि r = 3 सेमी. तथा r = 4 सेमी. है
View Solutionवृत|उदाहरण
View Solutionवृत पर आधारित प्रश्न
View Solutionनिम्नलिखित कथनो में सत्य एवं असत्य कथन की पहचान करे (2sqrt5)/(3sqrt15) एक अपरिमेय संख्या है
View Solutionपिछले वर्ष के बोर्ड्स परीक्षाओ में वृत पर आधारित प्रश्न
View SolutionBoards 2021|वृत की स्पर्श रेखा#!#Revision
View SolutionBoards 2021|आइये जाने एक बिंदु से वृत पर स्पर्श रेखा के बारे में#!#वृत#!#Revision
View Solutionवृत
View Solutionवृत
View Solutionवृत
View Solutionवृत
View Solutionवृत
View SolutionRevision|वृत#!#Quiz की सहायता से Revision
View Solution
