If nth division of main scale coincides with (n+1)th divisions of vernier scale. Given one main scale division is equal to 'a' units. Find the least count of the vernier.
To find the least count of the Vernier scale given that the nth division of the main scale coincides with the (n+1)th division of the Vernier scale, we can follow these steps:
1. Understand the Given Information:
- We know that one main scale division (MSD) is equal to a units.
- The nth division of the main scale coincides with the (n+1)th division of the Vernier scale.
2. Express the Coinciding Divisions:
- Since the nth MSD coincides with the (n+1)th Vernier scale division (VSD), we can express this relationship mathematically:
n MSD=(n+1) VSD
3. Substitute the Value of MSD:
- We know that 1 MSD=a units, so:
n⋅a=(n+1) VSD
4. Solve for VSD:
- Rearranging the equation gives:
VSD=n⋅an+1
5. Calculate the Least Count of the Vernier Scale:
- The least count (LC) of the Vernier scale is defined as:
LC=1 MSD−1 VSD
- Substituting the values we have:
LC=a−n⋅an+1
6. Simplify the Expression:
- To simplify, factor out a:
LC=a(1−nn+1)
- This can be simplified further:
LC=a((n+1)−nn+1)=a(1n+1)
7. Final Result:
- Therefore, the least count of the Vernier scale is:
LC=an+1
Summary:
The least count of the Vernier scale is given by an+1.
- We know that one main scale division (MSD) is equal to a units.
- The nth division of the main scale coincides with the (n+1)th division of the Vernier scale.
- Since the nth MSD coincides with the (n+1)th Vernier scale division (VSD), we can express this relationship mathematically:
n MSD=(n+1) VSD
- We know that 1 MSD=a units, so:
n⋅a=(n+1) VSD
- Rearranging the equation gives:
VSD=n⋅an+1
- The least count (LC) of the Vernier scale is defined as:
LC=1 MSD−1 VSD
- Substituting the values we have:
LC=a−n⋅an+1
- To simplify, factor out a:
LC=a(1−nn+1)
- This can be simplified further:
LC=a((n+1)−nn+1)=a(1n+1)
- Therefore, the least count of the Vernier scale is:
LC=an+1
The least count of the Vernier scale is given by an+1.
Topper's Solved these Questions
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.1
2 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.2
2 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
Similar Questions
N divisions on the main scale of a vernier callipers coincide with (N + 1) divisions on the vernier scale. If each division on the main scale is 'a' units, then the least count of the instrument is
View SolutionIn vernier callipers, m divisions of main scale with (m+1) divisions of vernier scale. If each division of main scale is d units, the least count of the instrument is
View SolutionIn a vernier callipers n divisions of its main scale match with (n+5) divisions on its vernier scale. Each division of the main scale is of x unit. Using the vernier principle, find the least count.
View SolutionIn a vernier callipers, n divisions of its main scale match with (n+1) divisions on its vernier scale. Each division of the main scale is a units. Using the vernier principle, calculate its least count.
View Solution19 divisions on the main scale of a vernier calipers coincide with 20 divisions on the vernier scale. If each division on the main scale is of 1cm, determine the least count of instrument.
View SolutionIn a given slide callipers 10 division of its vernier coincides with its 9 main scale divisions. If one main scale division is equal to 0.5 mm then find its least count.
View Solutionin an experiment the angles are required to be using an instrument, 29 divisions of the main scale exactly coincide with the 30 divisions of the vernier scale. If the sallest division of the main scale is half- a degree (=0.5∘, then the least count of the instrument is :
View SolutionIn an instrument, there are 25 divisions on the vernier scale which have length of 24 divisions of the main scale. 1 cm on main scale is divided in 20 equal parts. Find the least count.
View SolutionThe edge of a cube is measured using a vernier callipers. [9 divisions of the main scale is equal to 10 divisions of the vernier scale and 1 main scale dividsion is 1mm]. The main scale division reading is 10 and 1st division of vernier scale was found to be coinciding with the main scale. The mass of the cube is 2.736g. Calculate the density in g/cm3 upto correct significant figures.
View SolutionThe figure shows the variation of energy with the orbit radius of a body in circular planetary motion.
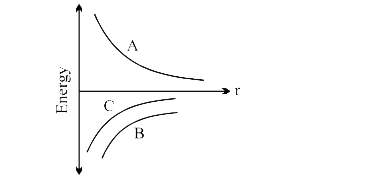
Find the correct statement about the curves A, B and C
View Solution
