A student performs an experiment to determine the Young's modulus of a wire, exactly2m long, by Searle's method. In a partcular reading, the student measures the extension in the length of the wire to be 0.8mm with an uncertainty of ±0.05mm at a load of exactly 1.0kg, the student also measures the diameter of the wire to be 0.4mm with an uncertainty of ±0.01mm. Take g=9.8m/s2 (exact). the Young's modulus obtained from the reading is
The correct Answer is:A, B, D
To determine the Young's modulus of a wire using the provided data, we can follow these steps:
Step 1: Understand the formula for Young's modulus
The formula for Young's modulus (Y) is given by:
Y=F⋅LA⋅ΔL
Where:
- F is the force applied (in Newtons),
- L is the original length of the wire (in meters),
- A is the cross-sectional area of the wire (in square meters),
- ΔL is the extension of the wire (in meters).
Step 2: Convert the measurements to SI units
1. Length of the wire (L): Given as 2 m (already in SI units).
2. Extension (ΔL): Given as 0.8 mm, which needs to be converted to meters:
ΔL=0.8mm=0.8×10−3m=0.0008m
3. Diameter of the wire (d): Given as 0.4 mm, which needs to be converted to meters:
d=0.4mm=0.4×10−3m=0.0004m
Step 3: Calculate the force (F)
The force is the weight of the load applied, which can be calculated using:
F=m⋅g
Where:
- m=1.0kg
- g=9.8m/s2
Calculating the force:
F=1.0kg⋅9.8m/s2=9.8N
Step 4: Calculate the cross-sectional area (A)
The cross-sectional area of the wire can be calculated using the formula for the area of a circle:
A=π(d2)2
Calculating the area:
A=π(0.00042)2=π(0.0002)2=π⋅0.00000004≈3.14⋅0.00000004≈1.256×10−7m2
Step 5: Substitute the values into the Young's modulus formula
Now we can substitute the values into the Young's modulus formula:
Y=9.8N⋅2m1.256×10−7m2⋅0.0008m
Calculating the denominator:
1.256×10−7⋅0.0008=1.0048×10−10m3
Now substituting back:
Y=19.61.0048×10−10≈1.95×1011N/m2
Step 6: Calculate the uncertainty in Young's modulus
The relative uncertainty in Young's modulus can be calculated using the formula:
ΔYY=2Δdd+ΔLL
Where:
- Δd=0.01mm=0.01×10−3m=0.00001m
- ΔL=0.05mm=0.05×10−3m=0.00005m
Calculating the relative uncertainties:
Δdd=0.000010.0004=0.025
ΔLL=0.000050.0008=0.0625
Now substituting into the relative uncertainty formula:
ΔYY=2(0.025)+0.0625=0.1125
Calculating the uncertainty:
ΔY=0.1125×1.95×1011≈2.2×1010N/m2
Final Result
Thus, the Young's modulus obtained from the reading is:
Y=1.95×1011±2.2×1010N/m2
The formula for Young's modulus (Y) is given by:
- F is the force applied (in Newtons),
- L is the original length of the wire (in meters),
- A is the cross-sectional area of the wire (in square meters),
- ΔL is the extension of the wire (in meters).
1. Length of the wire (L): Given as 2 m (already in SI units).
2. Extension (ΔL): Given as 0.8 mm, which needs to be converted to meters:
ΔL=0.8mm=0.8×10−3m=0.0008m
3. Diameter of the wire (d): Given as 0.4 mm, which needs to be converted to meters:
d=0.4mm=0.4×10−3m=0.0004m
The force is the weight of the load applied, which can be calculated using:
F=m⋅g
Where:
- m=1.0kg
- g=9.8m/s2
F=1.0kg⋅9.8m/s2=9.8N
The cross-sectional area of the wire can be calculated using the formula for the area of a circle:
A=π(d2)2
Calculating the area:
A=π(0.00042)2=π(0.0002)2=π⋅0.00000004≈3.14⋅0.00000004≈1.256×10−7m2
Now we can substitute the values into the Young's modulus formula:
Y=9.8N⋅2m1.256×10−7m2⋅0.0008m
1.256×10−7⋅0.0008=1.0048×10−10m3
Y=19.61.0048×10−10≈1.95×1011N/m2
The relative uncertainty in Young's modulus can be calculated using the formula:
ΔYY=2Δdd+ΔLL
- Δd=0.01mm=0.01×10−3m=0.00001m
- ΔL=0.05mm=0.05×10−3m=0.00005m
Δdd=0.000010.0004=0.025
ΔLL=0.000050.0008=0.0625
ΔYY=2(0.025)+0.0625=0.1125
ΔY=0.1125×1.95×1011≈2.2×1010N/m2
Thus, the Young's modulus obtained from the reading is:
Y=1.95×1011±2.2×1010N/m2
Topper's Solved these Questions
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Exercise 3.5
Explore 2 Videos
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Exercise 3.6
Explore 3 Videos
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Exercise 3.3
Explore 8 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Integer
Explore 17 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Medical entranes gallery
Explore 49 Videos
Similar Questions
A student measured the diameter of a wire using a screw gauge with least count 0.001cm and listed the measurement. The correct measurement is
View SolutionA wire of length 15m and diameter 4 mm elongates 0.3mm when stretched by weigth of 2.20kg. Calulate the Young's modulus of the material of the wire.
View SolutionA cubic cm of gold is drawn into a wire 0.1 mm in diameter, find the length of the wire.
View SolutionA wire 4m long 0.3 mm diameter is streteched by a force of 8 kg.wt. If the extension in the length amounts to 1.5 mm, calcualte the energy stored in the wire?
View SolutionWhen a screw gauge of least count 0.01 mm is used to measure the diameter of a wire, the reading on the sleeve is found to be 1 mm and the reading on the thimble is found to be 27 divisions.What is the diameter of the wire in cm ?
View SolutionA uniform wire of length 8m and diameter 0.6mm stretched by 4mm under a certain force. If the Poisson's ratio of the material of the wrie is 0.3, calculate the change in diameter of the wire.
View SolutionFor the experimental determination of Young.s modulus of elasticity Y of the material of a given wire by using Searle.s apparatus, the spherometer reading while load increasing and decreasing are tabulated below:
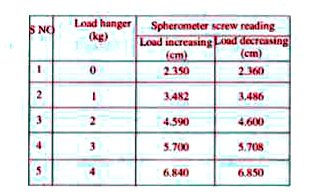
The mean extension for 2kg load is
View SolutionIn an experiment on the determination of young's Modulus of a wire by Searle's method , following data is available:
Normal length of the wire (L)=110cm
Diameter of the wire (d)=0.01cm
Elongation in the wire (l)=0.125cm
This elongation is for a tension of 50N. The least counts for corresponding quantities are 0.01cm,0.00005cm,and0.001cm , respectively. Calculate the maximum error in calculating the value of Young's modulus (Y).
View SolutionResistance of a metal wire of length 1 m is 26Ω at 20∘C. If the diameter of the wire is 0.3mm, what will be the resistivity of the metal at that temperature ? .
View SolutionOne end of a wire 2m long and 0.2 cm^2 in cross section is fixed in a ceiling and a load of 4.8 kg is attached to the free end. Find the extension of the wire. Young modulus of steel =2.0×1011Nm−2. Take g=10ms−2.
View Solution