A fixed mortar fires a bomb at an angle of above the horizontal with a muzzle velocity of . A tank is advancing directly towards the mortar on level ground at a constant speed of . The initial separation (at the instant mortar is fired) between the mortar and tank, so that the tank would be hit is
662.4m
526.3m
486.6m
None of these
The correct Answer is:D
To solve the problem, we need to find the initial separation between the mortar and the tank so that the tank is hit when the bomb is fired. We will break down the solution into steps.
Step 1: Calculate the Time of Flight of the Projectile
The time of flight (T) for a projectile launched at an angle θ with an initial velocity u is given by the formula:
T=2usinθg
Where:
- u=80m/s (muzzle velocity)
- θ=53∘
- g=10m/s2 (acceleration due to gravity)
First, we need to calculate sin53∘. Using a calculator or trigonometric tables, we find:
sin53∘≈0.7986
Now substituting the values into the formula:
T=2×80×0.798610=127.77610=12.7776s≈12.8s
Step 2: Calculate the Distance Traveled by the Tank
The tank is moving towards the mortar at a constant speed of 5m/s. The distance (x) the tank travels in time T is given by:
x=speed×time=5m/s×12.8s=64m
Step 3: Calculate the Range of the Projectile
The range (R) of a projectile is given by the formula:
R=u2sin2θg
Where:
- sin2θ=sin(106∘)
Using the double angle formula:
sin2θ=2sin53∘cos53∘
We already know sin53∘≈0.7986 and cos53∘≈0.6018.
Calculating sin2θ:
sin2θ=2×0.7986×0.6018≈0.9607
Now substituting into the range formula:
R=802×0.960710=6400×0.960710=614.4m
Step 4: Calculate the Initial Separation
The initial separation (S) between the mortar and the tank when the bomb is fired is the sum of the range of the projectile and the distance traveled by the tank:
S=R+x=614.4m+64m=678.4m
Final Answer
The initial separation between the mortar and the tank so that the tank would be hit is approximately 678.4m.
---
The time of flight (T) for a projectile launched at an angle θ with an initial velocity u is given by the formula:
T=2usinθg
Where:
- u=80m/s (muzzle velocity)
- θ=53∘
- g=10m/s2 (acceleration due to gravity)
sin53∘≈0.7986
T=2×80×0.798610=127.77610=12.7776s≈12.8s
The tank is moving towards the mortar at a constant speed of 5m/s. The distance (x) the tank travels in time T is given by:
x=speed×time=5m/s×12.8s=64m
The range (R) of a projectile is given by the formula:
R=u2sin2θg
Where:
- sin2θ=sin(106∘)
sin2θ=2sin53∘cos53∘
We already know sin53∘≈0.7986 and cos53∘≈0.6018.
sin2θ=2×0.7986×0.6018≈0.9607
R=802×0.960710=6400×0.960710=614.4m
The initial separation (S) between the mortar and the tank when the bomb is fired is the sum of the range of the projectile and the distance traveled by the tank:
S=R+x=614.4m+64m=678.4m
The initial separation between the mortar and the tank so that the tank would be hit is approximately 678.4m.
Topper's Solved these Questions
- PROJECTILE MOTIONBook:DC PANDEY ENGLISHChapter:PROJECTILE MOTIONExercise:Level - 1 Subjective
Explore 21 Videos
- PROJECTILE MOTIONBook:DC PANDEY ENGLISHChapter:PROJECTILE MOTIONExercise:Level - 2 Single Correct
Explore 10 Videos
- PROJECTILE MOTIONBook:DC PANDEY ENGLISHChapter:PROJECTILE MOTIONExercise:Level - 1 Assertion And Reason
Explore 10 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:(C )Medical entrances gallery
Explore 32 Videos
- PROPERTIES OF MATTERBook:DC PANDEY ENGLISHChapter:PROPERTIES OF MATTERExercise:Integer
Explore 8 Videos
Similar Questions
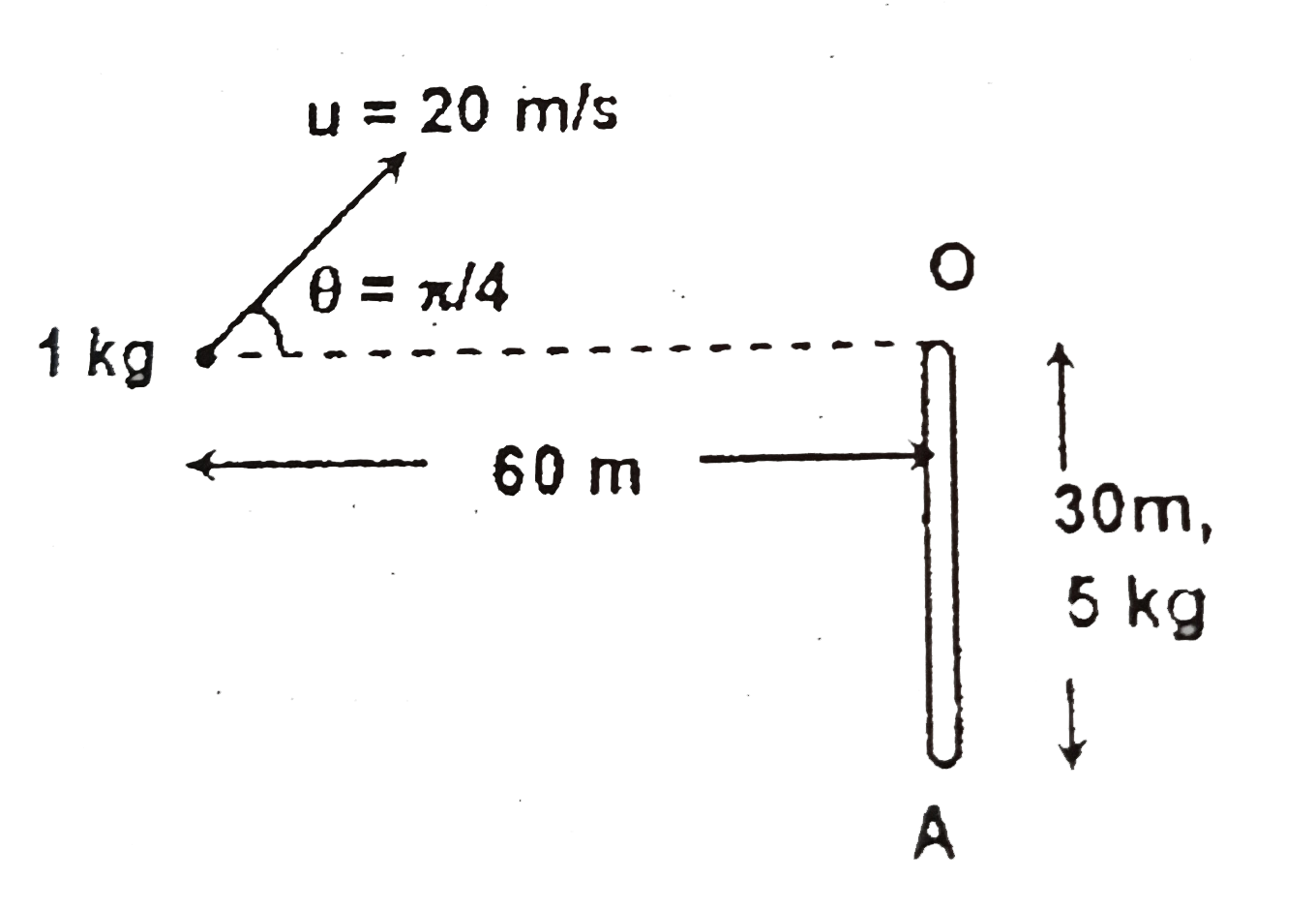
A particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
If projectile is fired horizontally, it will
View SolutionA projectile is thrown with a velocity of 10ms−1 at an angle of 60∘ with horizontal. The interval between the moments when speed is √5gm/s is (Take, g=10ms−2)
View SolutionA ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
View SolutionThe surface of water in a water tank on the top of a house is 4 m above the tap level. Find the pressure of water at the tap, when the tap is closed. Is it necessary to specify that the tap is closed? Take g=10ms−2
View SolutionConsider a shell that has a muzzle velocity of 45ms−1 fired from the tail gun of an airplane moving horizontally with a velocity of 215ms−1 . The tail gun can be directed at any angle with the vertical in the plane of motion of the airplane. The shell is fired when the plane is above point A on ground, and the plane is above point B on ground when the shell hits the ground. (Assume for simplicity that the Earth is flat)
View SolutionA stone is projected vertically up from the ground with velocity 40ms−1 . The interval of time between the two instants at which the stone is at a height of 60 m above the ground is (g=10ms−2)
View SolutionA lift, initially at rest on the ground, starts ascending with constant acceleration 8m/s2 After 0.5 seconds, a bolt falls off the floor of the lift. The velocity of the lift at the instant the bolt hits the ground is m/s .[Take g=10m/s2]
View SolutionA projectile is fired from a gun at an angle of 45∘ with the horizontal and with a speed of 20m/s relative to ground. At the highest point in its flight the projectile explodes into two fragments of equal masses. One fragement, whose initial speed is zero falls vertically. How far from the gun does the other fragment land, assuming a level terrain? Take g=10m/s2?
View SolutionA jet aeroplane is flying at a constant height of 2 km with a speed 360kmh−1 above the ground towards a target and releases a bomb. After how much time it will hit the target and what will be the horizontal distance of the aeroplane from the target so that the bomb should hit the target ? (Take g=10ms−2)
View SolutionA golfer standing on level ground hits a ball with a velocity of 52ms−1 at an angle θ above the horizontal. If tanθ=5/12, then find the time for which then ball is atleast 15m above the ground (takeg=10ms−2).
View Solution
