A projectile aimed at a mark, which is in the horizontal plane through the point of projection, falls a cm short of it when the elevation is α and goes b cm far when the elevation is β. Show that, if the speed of projection is same in all the cases the proper elevation is
12sin−1[bsin2α+asin2βa+b] .
The correct Answer is:A
To solve the problem, we need to analyze the projectile motion of an object launched at different angles and determine the proper elevation angle that would allow it to hit a target. The projectile falls short of the target by a distance a when launched at an angle α and goes beyond the target by a distance b when launched at an angle β.
1. Understanding the Range of a Projectile:
The range R of a projectile launched with an initial speed u at an angle θ is given by the formula:
R=u2sin(2θ)g
where g is the acceleration due to gravity.
2. Setting Up the Equations:
- When the projectile is launched at angle α, it falls short of the target by a:
R1=R−a=u2sin(2α)g
- When the projectile is launched at angle β, it goes beyond the target by b:
R2=R+b=u2sin(2β)g
3. Expressing Ranges in Terms of R:
From the above equations, we can express R in terms of R1 and R2:
R=R1+aandR=R2−b
4. Equating the Two Expressions for R:
Setting the two expressions for R equal gives:
R1+a=R2−b
5. Substituting the Ranges:
Substituting the expressions for R1 and R2:
u2sin(2α)g+a=u2sin(2β)g−b
6. Rearranging the Equation:
Rearranging the equation gives:
u2sin(2β)g−u2sin(2α)g=a+b
7. Factoring Out Common Terms:
Factoring out u2g:
u2g(sin(2β)−sin(2α))=a+b
8. Finding the Proper Elevation:
We want to find the angle θ such that:
R=u2sin(2θ)g
Using the previous results, we can express R in terms of a and b:
R=u2g⋅bsin(2α)+asin(2β)a+b
9. Final Expression for the Angle:
Setting the two expressions for R equal gives:
sin(2θ)=bsin(2α)+asin(2β)a+b
Therefore, the proper elevation angle θ is:
θ=12sin−1(bsin(2α)+asin(2β)a+b)
Final Answer:
θ=12sin−1(bsin(2α)+asin(2β)a+b)
The range R of a projectile launched with an initial speed u at an angle θ is given by the formula:
R=u2sin(2θ)g
where g is the acceleration due to gravity.
- When the projectile is launched at angle α, it falls short of the target by a:
R1=R−a=u2sin(2α)g
- When the projectile is launched at angle β, it goes beyond the target by b:
R2=R+b=u2sin(2β)g
From the above equations, we can express R in terms of R1 and R2:
R=R1+aandR=R2−b
Setting the two expressions for R equal gives:
R1+a=R2−b
Substituting the expressions for R1 and R2:
u2sin(2α)g+a=u2sin(2β)g−b
Rearranging the equation gives:
u2sin(2β)g−u2sin(2α)g=a+b
Factoring out u2g:
u2g(sin(2β)−sin(2α))=a+b
We want to find the angle θ such that:
R=u2sin(2θ)g
Using the previous results, we can express R in terms of a and b:
R=u2g⋅bsin(2α)+asin(2β)a+b
Setting the two expressions for R equal gives:
sin(2θ)=bsin(2α)+asin(2β)a+b
Therefore, the proper elevation angle θ is:
θ=12sin−1(bsin(2α)+asin(2β)a+b)
θ=12sin−1(bsin(2α)+asin(2β)a+b)
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Single Correct
10 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Single Correct
16 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A projectile is aimed at a mark on a horizontal plane through the point of projection and falls 6 m short when its elevation is 30° but overshoots the mark by 9 m when its elevation is 45∘. The angle of elevation of projectile to hit the target on the horizontal plane is :
View SolutionA particle projected with velcoity v0 strikes at right α plane through the point of projection .
View Solution
Knowledge Check
Two projectiles A and B thrown with speeds in the ratio 1 : √2 acquired the same heights. If A is thrown at an angle of 45∘ with the horizontal, the angle of projection of B will be
A0∘B60∘C30∘D45∘
The angle of elevation of the top of a tower from a pointA due south of the tower is α and from B due east of tower is β. If AB=d, show that the height of the tower is d√cot2α+cot2β.
View SolutionThe angle of elevation of the top of a tower from a pointA due south of the tower is α and from B due east of tower is β. If AB=d, show that the height of the tower is d√cot2α+cot2β.
View SolutionTwo bodies are projected from the same point with equal speeds in such directions that they both strike the same point on a plane whose inclination is β. If α the angle of projection of the first body with the horizontal , show that the ratio of their time of flights is sin(α−β)cosα
View SolutionThe elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is ABsinαsinβ√sin2α−sin2β
View SolutionA straight line passes through the point (α,β) and this point bisects the portion of the line intercepted between the axes. Show that the equation of the straight line is x2α+y2β=1.
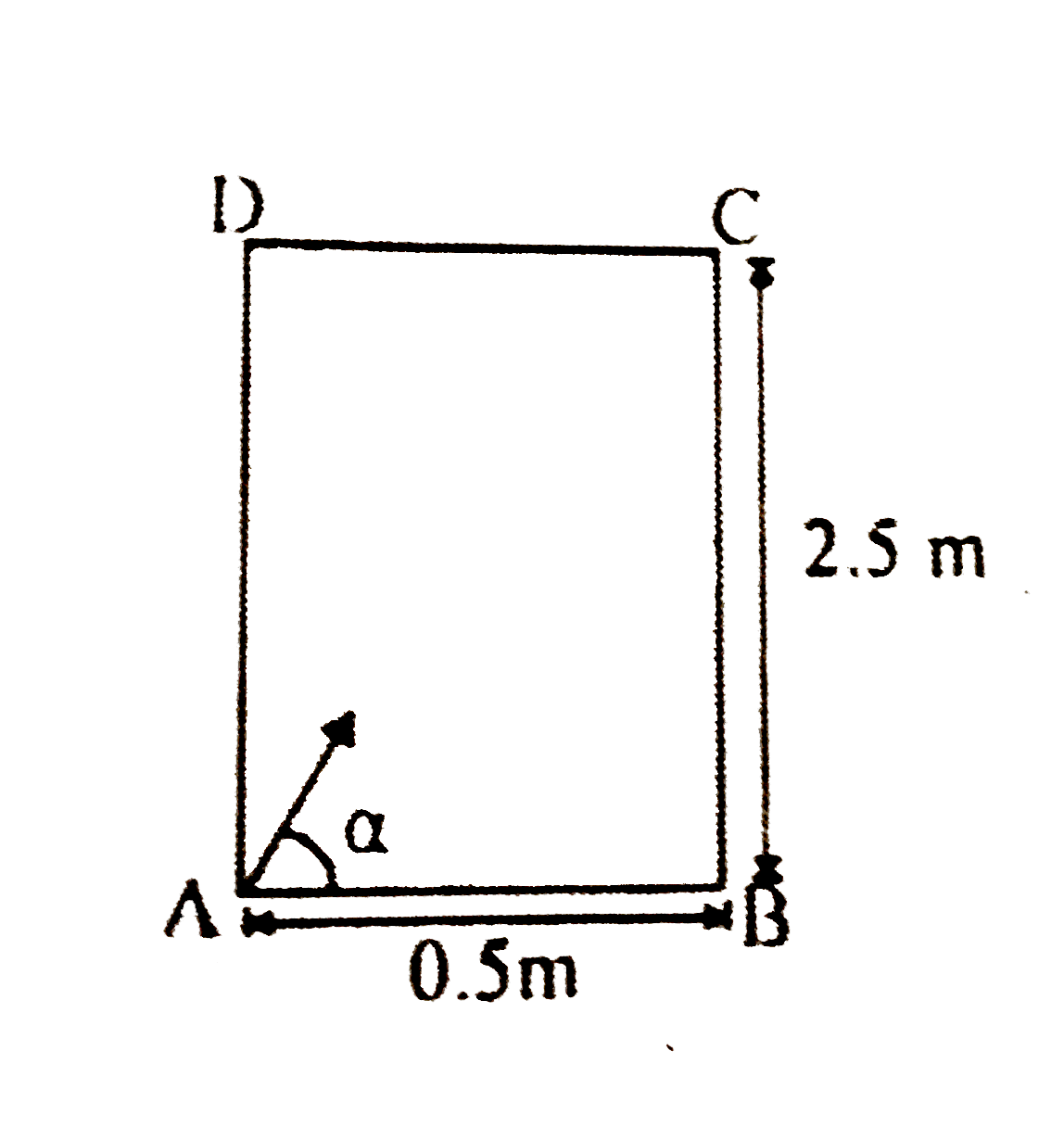
View SolutionA cuboidal elevator cabon is shown in the figure. A ball is thrown from point A on the floor of cabon when the elevator is falling under gravity. The plane of motions is ABCD and the angle of projection of the ball with AB, relative to elevator, if the ball collides with point C, is α. Then find the value of tanα.
View SolutionA stone projected from ground with certain speed at an angle θ with horizontal attains maximum height h1 when it is projected with same speed at an angle θ with vertical attains height h2. The horizontal range of projectile is
View Solution
