A particle moves along the x-axis from x=0 to x=5m under the influence of a given by F=7−2x+3x2. The work done by the applied force to the particle is.
a)360J
b)85J
c)185J
d)135J
The correct Answer is:D
To solve the problem, we need to calculate the work done by the force F=7−2x+3x2 as the particle moves from x=0 to x=5 meters. The work done by a force is given by the integral of the force over the distance moved.
1. Write the expression for work done:
The work done W by the force F when moving from x=a to x=b is given by:
W=∫baFdx
In this case, a=0 and b=5, so:
W=∫50(7−2x+3x2)dx
2. Integrate the force function:
We will integrate the function term by term:
W=∫507dx−∫502xdx+∫503x2dx
3. Calculate each integral:
- For the first term:
∫7dx=7x∣∣50=7(5)−7(0)=35
- For the second term:
∫2xdx=x2∣∣50=52−02=25
- For the third term:
∫3x2dx=x3∣∣50=53−03=125
4. Combine the results:
Now substituting back into the expression for work:
W=35−25+125
5. Calculate the final work done:
W=35−25+125=135Joules
Final Answer:
The work done by the applied force on the particle is 135Joules.
The work done W by the force F when moving from x=a to x=b is given by:
W=∫baFdx
In this case, a=0 and b=5, so:
W=∫50(7−2x+3x2)dx
We will integrate the function term by term:
W=∫507dx−∫502xdx+∫503x2dx
- For the first term:
∫7dx=7x∣∣50=7(5)−7(0)=35
- For the second term:
∫2xdx=x2∣∣50=52−02=25
- For the third term:
∫3x2dx=x3∣∣50=53−03=125
Now substituting back into the expression for work:
W=35−25+125
W=35−25+125=135Joules
The work done by the applied force on the particle is 135Joules.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective27videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Objective30videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion And Reason12videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
A particle moves along the X-axis from x=0 to x=5 m under the influence of a force given by F=7−2x+3x2. Find the work done in the process.
View SolutionA particle moves along the X-axis x=0 to x=5 m under the influence of a force given by F=10−2x+3x2. Work done in the process is
View SolutionA particle moves along X-axis from x=0 to x=1 m under the influence of a force given by F=3x2+2x−10. Work done in the process is
View SolutionA particle moves along X-axis from x=0 to x=1 m under the influence of a force given by F=3x2+2x−10. Work done in the process is
View SolutionA particle moves along x-axis from x=0 to x=2 m under the influence of a force F (in N) given by F=3x2+2x−5. Calculate the work done
View SolutionA force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
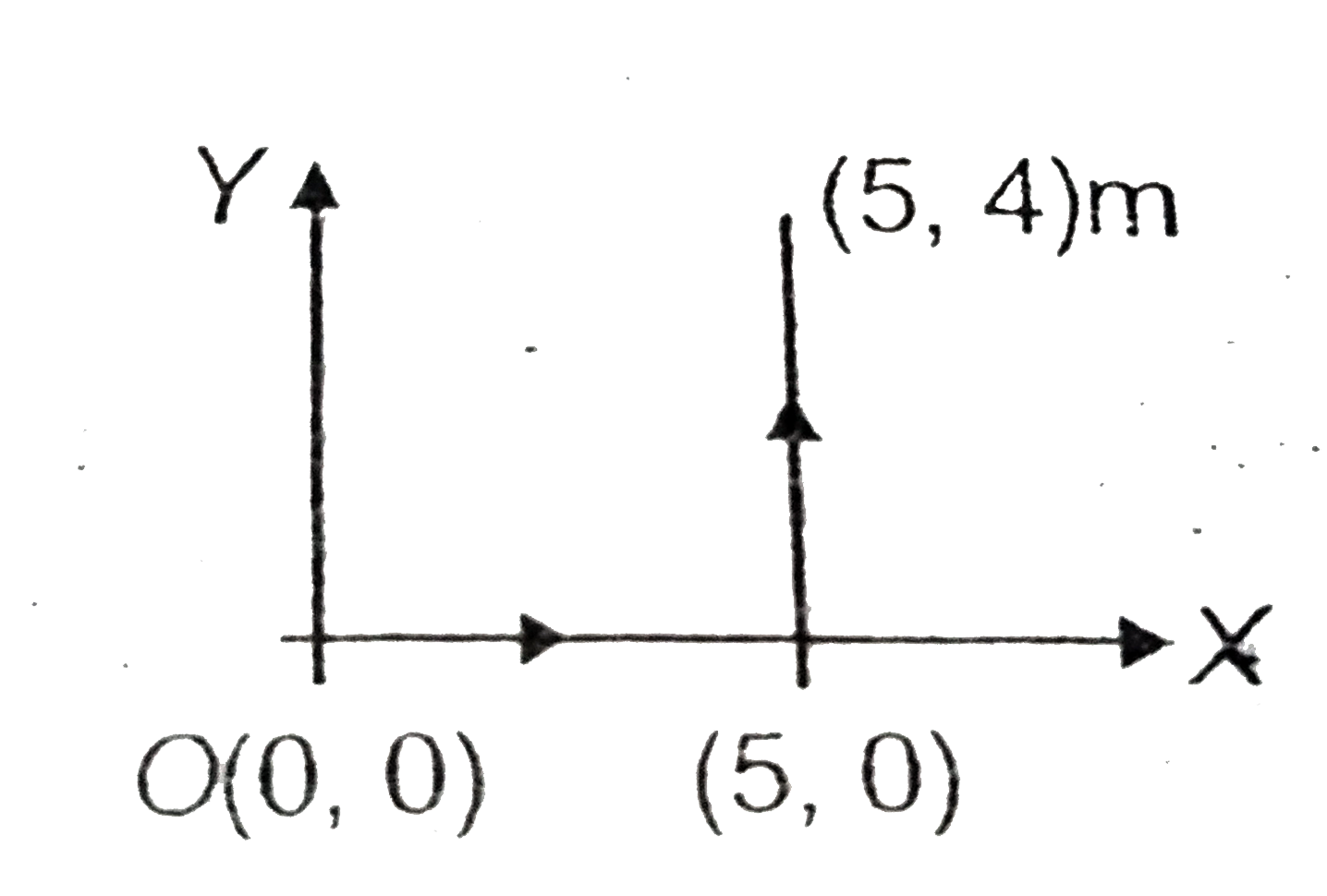 View Solution
View SolutionA particle is moving along the axis under the influnence of a force given by F=−5x+15. At time t=0, the particle is located at x=6 and having zero velocity it take 0.5 second to reach the origin for the first time. The equation of motion of the particle can be respected by
View SolutionA particle moves along x - axis under the action of a position dependent force F=(5x2−2x)N. Work done by force on the particle when it moves from origin to x = 3 m is
View SolutionA particle moves from a point (2m,3m,0) to (3m,2m,0) under the action of force of magnitude 5N acting along the line y=x. The work done by the force on the particle during the displacement is
View SolutionA force F=−k(^ˆi+xˆj) (where k is a positive constant) acts on a particle moving in the x−y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
(a) −2ka2 , (b) 2ka2,(c)-ka^(2),(d)ka^(2)View Solution

