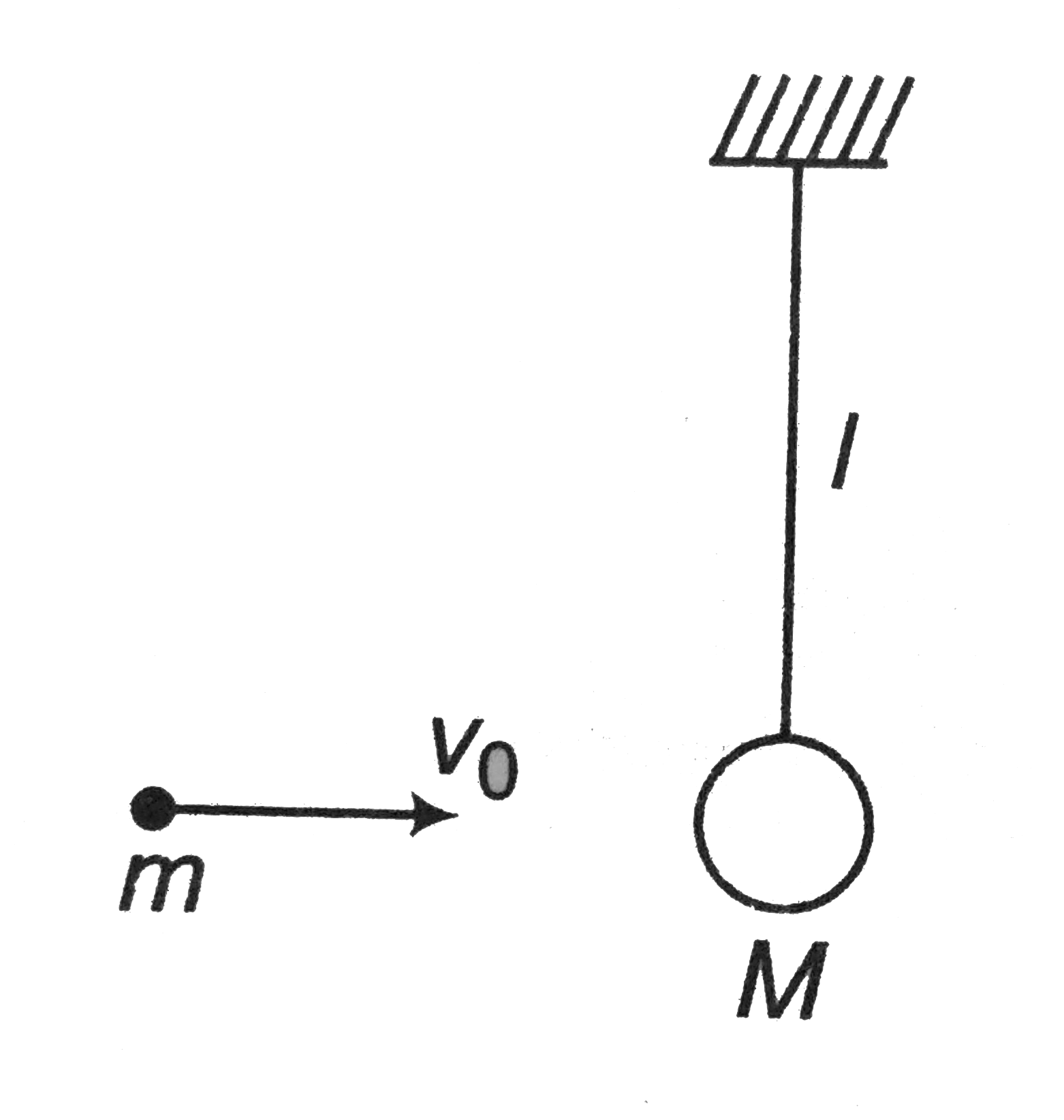
In the situation discussed above, find
(a) velocity of combined mass just after collision at the bottommost point (oru).
(b) loss of mechanical energy during collision.
(c) minimum value of v0 so that the combined mass completes the vertical circular motion.
The correct Answer is:A, B
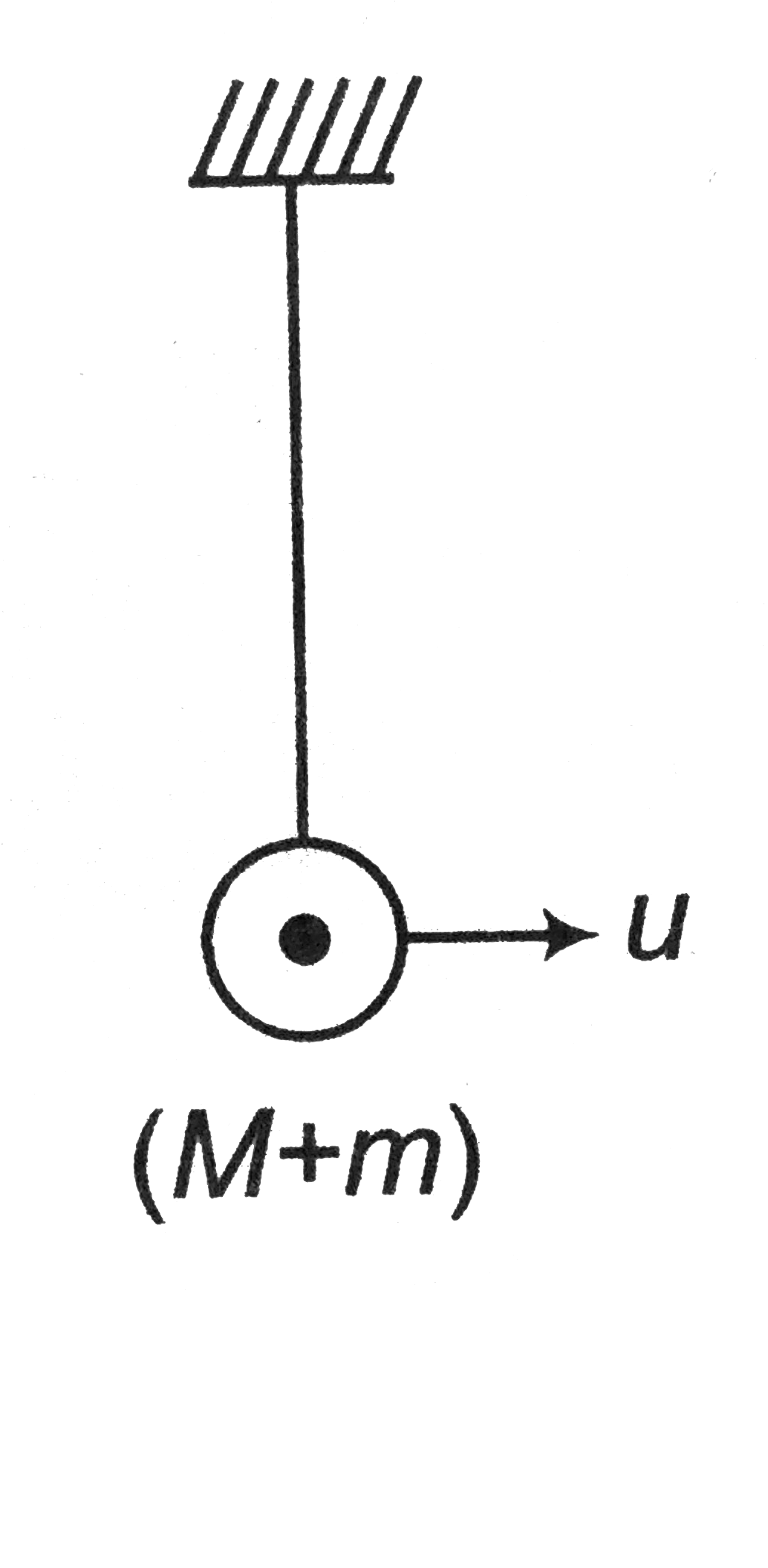
(a) Appying conservation of linear momentum, just before and just after collision.
pi=pf⇒mv0=(M+m)u⇒u=mv0M+m
(b) Loss of mechanical energy during collision,
=Ei−Ef (E=mechanical energy)
=12mv0−12(M+m)u2
=12mv20−12(M+m)[mv0M+m]2
=12Mmv20(M+m)
(c) For completing the vertical circular motion, velocity at bottommost point, u≥√5gl
∴mv0M+m≥√5gl⇒∴v0≥M+mm√5gl
or (v0)min=M+mm√5gl
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - MiscellaneousExamples
9 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.1
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 1
1 Video
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
In the figure shown in the text, if the block is a cube of side a
find
(a). ω just after impact
(b). Loss of mechanical enegy during impact
(c) minimum value of v so as the block overcomes the obstacle and does not turn back.
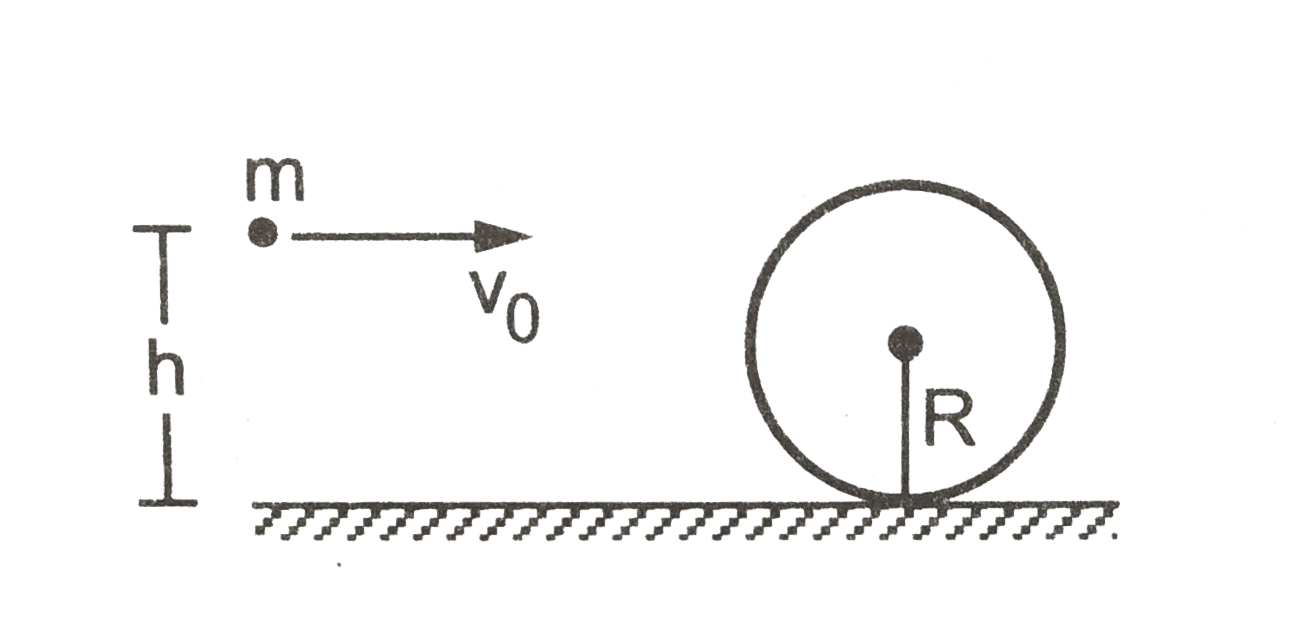
View SolutionThe sphere shown in figure lies on a rough plane when a particle of mass m travelling at a speed v0 collides and sticks with it. If the line of motion of the particle is at a distance h above the plane, find a. the linear speed o the combined system just after the collision b. the angular speed of the system about the centre of the sphere just the collision c. the value of h for which the sphere starts pure rolling on the plane Assume that the mass M of the sphere is large compared to the mass of the particle so that the centre of mass of the combined system is not appreciably shifted from the centre of the sphere.
View Solution
Knowledge Check
A bullet of mass 20g moving horizontally strikes a block of mass 480g suspended by a string of length 2m. If the collision is completely inelastic , the minimum velocity of bullet , so that the combined mass complete vertical circle should be
A100m/sB150m/sC200m/sD250m/s
The sphere shown in figue lies on a rough plane when a particle of mass m travbelling at a speed v0 collides and sticks with it. If the line of motion of the particle is at a distance h above the plane, find a. the linear speed o the combine dsystem just after teh collision b. the angular speed of the system about the centre of the sphere just the collistion c. the value of h for which the sphere starts pure rolling on the plane Assume that the mass M of the sphesre is large compared to teh mass of the partcle so that is large compared toteh mass of the particle so that teh centre of mass of the combined system is not appreciably shifted from the centre of the sphere.

View SolutionA wooden log of mass M and length L is hinged by a frictionless nail at O. A bullet of mass m strikes with velocity v and sticks to it. Find the angular velocity of the system, immediately after the collision about O. Also, calculate the minimum value of v so that log becomes horizontal after collision.
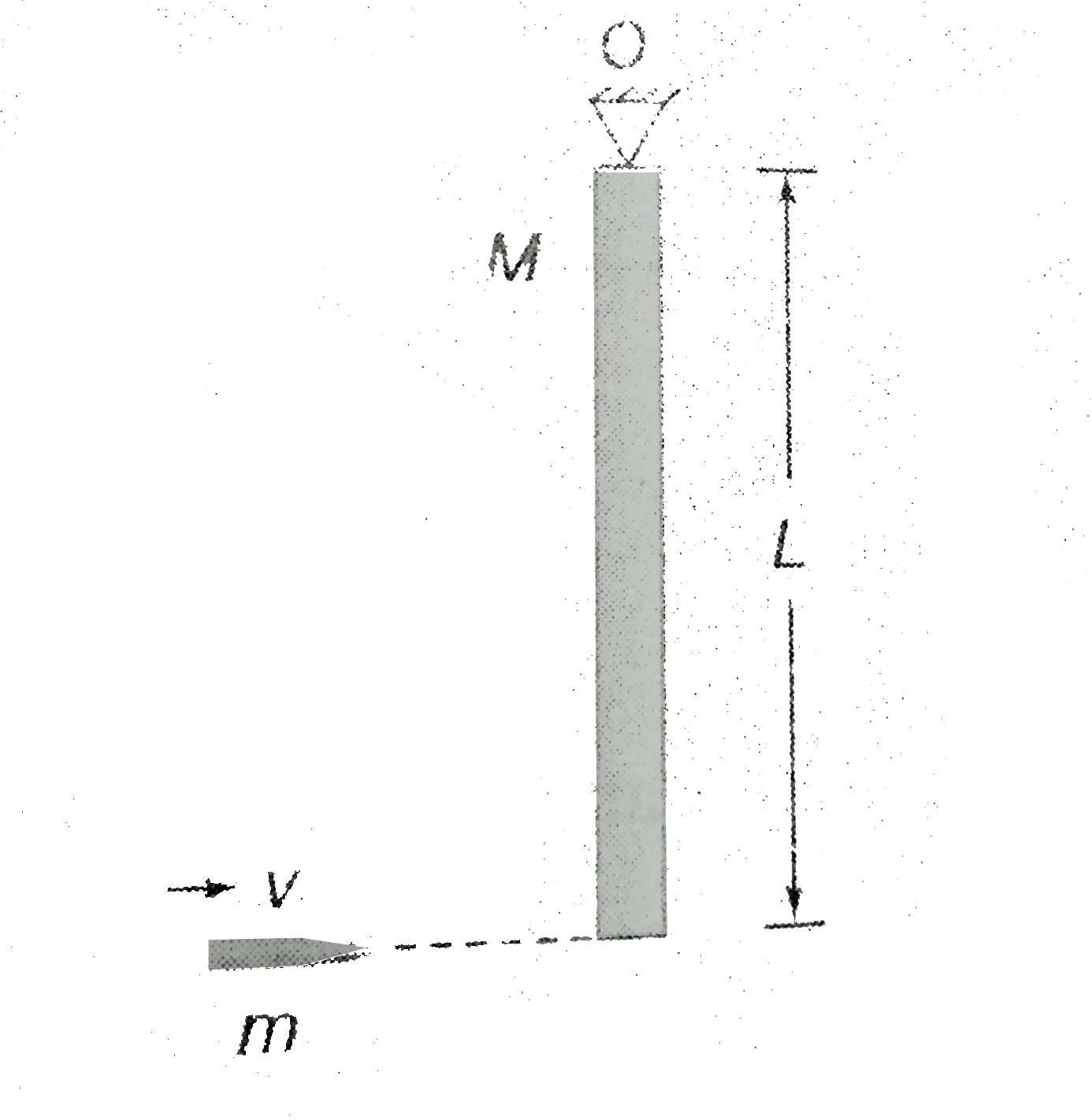
View SolutionSuppose the particle of the previous problem has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M. a. Find the velocity of the particle with respect to C of the system consituting the rod plus the particle. b. Find the velociyt of the particle with respect to C before the collision. c. Find the velocity of the rod with respect to C before the colision. e. find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. f. Find the velociyt of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
View SolutionTwo balls A and B. are of the sme size but the mass of A is double that of B. they move along the sme line in opposite direction. A with velocity 2μ and B with velocity 3μ If their total kinetoc energy after collision is half their total kinetic energy before collision find the coefficient of restitution. Find also their velocities after collision.
View SolutionConsider on object of mass m moving with velocity v0 and all other masses at rest initially. Find the % loss in energy after final collision. If all collision are perfectly inelastic.

View SolutionConsider on object of mass m moving with velocity v0 and all other masses at rest initially. Find the % loss in energy after final collision. If all collision are perfectly inelastic.

View SolutionConsider two satellites A and B of equal mass, moving in the same circular orbit of radius r around the earth but in the opposite sense and therefore a collision occurs.
(a) Find the total mechanical energy EA+EB of the two satellite-plus-earth system before collision.
(b) If the collision is completely inelastic, find the total mechanical energy immediately after collision. Describe the subsequent motion of the combined satellite.
View Solution
